题目内容
6.已知关于x的一元二次方程x2-2x+k-1=0.(1)若此方程有两个不相等的实数根,求实数k的取值范围;
(2)已知x=3是此方程的一个根,求方程的另一个根及k的值.
分析 (1)利用方程根与判别式的关系,得出根的判别式符号直接解不等式得出即可;
(2)将x=3代入,进而求出k的值,进而得出方程的解.
解答 解:(1)∵关于x的一元二次方程x2-2x+k-1=0有两个不相等的实数根,
∴b2-4ac=4-4(k-1)>0,
解得:k<2;
(2)∵x=3是此方程的一个根,
∴代入方程得:9-6+k-1=0,
解得:k=-2,
∴原方程为:x2-2x-3=0,
解得:x1=3,x2=-1.
点评 此题主要考查了一元二次方程的解以及根的判别式,利用方程根与判别式的关系得出是解题关键.

练习册系列答案
相关题目
14.计算1+(-2)+3+(-4)+5+(-6)得( )
| A. | 3 | B. | -3 | C. | 10 | D. | -10 |
1.若|x-2|+(y+5)2=0,则yx=( )
| A. | 10 | B. | -10 | C. | 25 | D. | -25 |
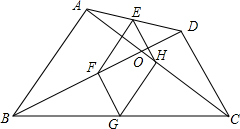 如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD,BD,BC,AC的中点.
如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD,BD,BC,AC的中点. AB是⊙O的直径,CD是任意一条非直径的弦,求证:AB>CD.
AB是⊙O的直径,CD是任意一条非直径的弦,求证:AB>CD.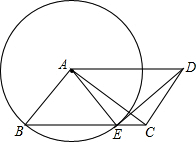 在平行四边形ABCD中,以点A为圆心,AB为半径的圆,交BC于点E.
在平行四边形ABCD中,以点A为圆心,AB为半径的圆,交BC于点E.