题目内容
3.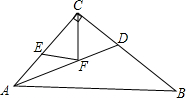 △ABC是等腰直角三角形,∠ACB=90°,AC=4,AD是角平分线,E,F分别是线段AC、AD上的动点,求EF+CF的最小值.
△ABC是等腰直角三角形,∠ACB=90°,AC=4,AD是角平分线,E,F分别是线段AC、AD上的动点,求EF+CF的最小值.
分析 由轴对称的性质可知:EC=EC′,所以EF+FC=EF+FC′,由垂线段最短可知:当C′E⊥AC时,C′E有最小值,然后利用锐角三角函数的定义即可求得EC′的长.
解答 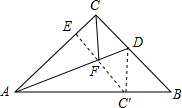 解:如图所示:将△ACD沿AD翻折得到△ADC′,连接DC′,过点C′作C′E⊥AC,
解:如图所示:将△ACD沿AD翻折得到△ADC′,连接DC′,过点C′作C′E⊥AC,
∵AD是∠CAB的角平分线,
∴△ACD与△ADC′关于AD对称.
∴点C′在AB上.
由翻折的性质可知:AC′=AC=4,.FC=FC′.
∴EF+FC=EF+FC′.
由垂线段最短可知:当C′E⊥AC时,C′E有最小值.
在Rt△ACB中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=4$\sqrt{2}$,
∵C′E⊥AC,
∴△AEC′是等腰直角三角形,
∴EC′=$\frac{\sqrt{2}}{2}$AC′=2$\sqrt{2}$.
∴EF+CF的最小值是2$\sqrt{2}$.
点评 本题主要考查的是翻折的性质、垂线段最短、勾股定理的应用,锐角三角函数的定义,明确当C′E⊥AC时,C′E有最小值是解题的关键.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
14.计算1+(-2)+3+(-4)+5+(-6)得( )
| A. | 3 | B. | -3 | C. | 10 | D. | -10 |
 AB是⊙O的直径,CD是任意一条非直径的弦,求证:AB>CD.
AB是⊙O的直径,CD是任意一条非直径的弦,求证:AB>CD.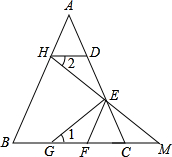 如图所示,在△ABC中,AB=AC,DE=EC,DH∥BA,EF∥AB,HE的延长线与BC的延长线相交于点M,点G在BC上,且∠1=∠2,证明:△EGM与△EFC是等腰三角形.
如图所示,在△ABC中,AB=AC,DE=EC,DH∥BA,EF∥AB,HE的延长线与BC的延长线相交于点M,点G在BC上,且∠1=∠2,证明:△EGM与△EFC是等腰三角形.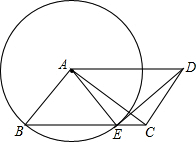 在平行四边形ABCD中,以点A为圆心,AB为半径的圆,交BC于点E.
在平行四边形ABCD中,以点A为圆心,AB为半径的圆,交BC于点E.