题目内容
5．
如图，把一张长方形的纸按图那样折叠后，B、D两点落在B′、D′点处，若∠1=70°，求∠2的度数．
分析 根据轴对称的性质可得∠B′OG=∠BOG，再根据∠AOB′=70°，可得出∠1的度数．
解答 解：根据轴对称的性质得：∠2=∠BOG，
∵∠1=70°，
∴∠B′OG+∠BOG=110°，
∴∠2=$\frac{1}{2}$×110°=55°．
点评 本题考查了角的计算以及翻折变换，注意翻折前后不变的边和角，是解此题的关键．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
15．
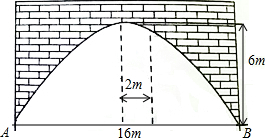如图，有一个抛物线型拱桥，桥洞离水面的最大高度为6m，跨度为16m，请建立适当的直角坐标系．
（1）求这条抛物线所对应的函数表达式；
（2）在这条抛物线的对称轴右边2m处，桥洞离水面的高度是多少？
如图，有一个抛物线型拱桥，桥洞离水面的最大高度为6m，跨度为16m，请建立适当的直角坐标系． （1）求这条抛物线所对应的函数表达式；
（2）在这条抛物线的对称轴右边2m处，桥洞离水面的高度是多少？
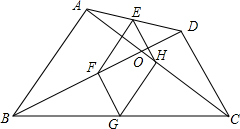如图，四边形ABCD中，对角线相交于点O，E、F、G、H分别是AD，BD，BC，AC的中点．
20．
如图，若a∥b，∠1=105°，则∠2的度数为（ ）
如图，若a∥b，∠1=105°，则∠2的度数为（ ）| A． | 55° | B． | 60° | C． | 65° | D． | 75° |
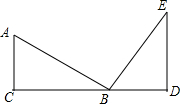如图，在△ABC中，∠C=90°，CB=4，延长CB至点D，使BD=AC，作∠BDE=90°，∠DBE=∠A，两角的另一边相交于点E，则DE的长为4．
14．计算1+（-2）+3+（-4）+5+（-6）得（ ）
| A． | 3 | B． | -3 | C． | 10 | D． | -10 |
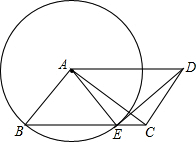在平行四边形ABCD中，以点A为圆心，AB为半径的圆，交BC于点E．