题目内容
18.已知x+y=2,2y2-y-4=0,则y-$\frac{x}{y}$的值为$\frac{3}{2}$.分析 根据x+y=2,得出x=2-y,再根据2y2-y-4=0,得出y-$\frac{2}{y}$=$\frac{1}{2}$,然后代入要求的式子进行计算即可得出答案.
解答 解:∵x+y=2,
∴x=2-y,
∵2y2-y-4=0,
∴2y-1-$\frac{4}{y}$=0
∴2y-$\frac{4}{y}$=1
∴y-$\frac{2}{y}$=$\frac{1}{2}$,
∴y-$\frac{x}{y}$=y-$\frac{2-y}{y}$=y-$\frac{2}{y}$+1=$\frac{1}{2}$+1=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 此题考查了分式的化简求值,关键是根据给出的式子进行变形得出y-$\frac{2}{y}$=$\frac{1}{2}$,注意要用整体代入法进行计算比较简单.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
6. 如图,点P为等边△ABC的边AB上一点,点Q为BC延长线上一点,PA=CQ,连接PQ交AC于D,若CD=3,BQ=10,则PA的长为( )
如图,点P为等边△ABC的边AB上一点,点Q为BC延长线上一点,PA=CQ,连接PQ交AC于D,若CD=3,BQ=10,则PA的长为( )
 如图,点P为等边△ABC的边AB上一点,点Q为BC延长线上一点,PA=CQ,连接PQ交AC于D,若CD=3,BQ=10,则PA的长为( )
如图,点P为等边△ABC的边AB上一点,点Q为BC延长线上一点,PA=CQ,连接PQ交AC于D,若CD=3,BQ=10,则PA的长为( )| A. | 2 | B. | 2.2 | C. | 2.5 | D. | 2.4 |
3.下列关于有理数的说法中,错误的是( )
| A. | 所有的整数都是有理数 | B. | 所有的分数都是有理数 | ||
| C. | 所有的无限小数都是有理数 | D. | 所有的有限小数都是有理数 |

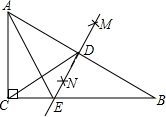 如图,在△ABC中,∠ACB=90°,分别以点A、点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD、AE,请你依作图信息写一个正确的结论AE=BE(答案不唯一).
如图,在△ABC中,∠ACB=90°,分别以点A、点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD、AE,请你依作图信息写一个正确的结论AE=BE(答案不唯一). 如图,在Rt△ABC中,∠ABC=60°,$BC=\sqrt{3}$.
如图,在Rt△ABC中,∠ABC=60°,$BC=\sqrt{3}$.