题目内容
6．
如图，点P为等边△ABC的边AB上一点，点Q为BC延长线上一点，PA=CQ，连接PQ交AC于D，若CD=3，BQ=10，则PA的长为（ ）| A． | 2 | B． | 2.2 | C． | 2.5 | D． | 2.4 |
分析 利用平行线的性质结合相似三角形的判定与性质得出即可．
解答 解：过点P作PF∥BC交AC于点F，如图1；
∵PF∥BC，
∴△APF∽△ABC，
∵△ABC是等边三角形，
∴△APF也是等边三角形，
∴∠APF=∠BCA=60°，AP=PF=AF=CQ，
∵CD=3，BQ=10，
∴2PA+6=10，
∴PA=2，
故选A
点评 本题考查了等边三角形的性质和判定，平行线的性质等知识点的应用，能综合运用性质进行推理是解此题的关键，
练习册系列答案
相关题目
16．已知某反比例函数的图象经过点（m，n），则它也一定经过（ ）
| A． | （m，-n） | B． | （-n，-m） | C． | （-m，n） | D． | （-n，m） |
17．用配方法解方程x2-$\frac{2}{3}$x+1=0，正确的是（ ）
| A． | （x-$\frac{2}{3}$）2=1，x1=$\frac{5}{3}$，x2=-$\frac{1}{3}$ | B． | （x-$\frac{2}{3}$）2=$\frac{4}{9}$，x=$\frac{2±\sqrt{3}}{2}$ | ||
| C． | （x-$\frac{2}{3}$）2=-$\frac{8}{9}$，原方程无实数解 | D． | （x-$\frac{1}{3}$）2=-$\frac{8}{9}$，原方程无实数解 |
14．下列说法正确的是（ ）
| A． | “任意画一个三角形，其内角和是360°”是随机事件 | |
| B． | “明天的降水概率为80%”，意味着明天降雨的可能性较大 | |
| C． | “某彩票中奖概率是1%”，表示买100张这种彩票一定会中奖 | |
| D． | 晓芳抛一枚硬币10次，有7次正面朝上，当她抛第11次时，正面向上的概率为$\frac{7}{10}$ |
15．计算（-12）-（-3）+（-10）-（-9）-$\frac{1}{3}$的结果是（ ）
| A． | $-\frac{25}{3}$ | B． | $-\frac{43}{3}$ | C． | $-\frac{49}{3}$ | D． | $-\frac{31}{3}$ |
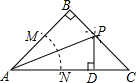如图，在等腰直角△ABC中，B=90°，以点A为圆心任意长为半径画弧，与AB，AC分别交于点M，N，分别以点M，N为圆心大于$\frac{1}{2}$MN长为半径画弧，两弧交于点P，且点P刚好落在边BC上，AB=10cm，下列说法中：