题目内容
2.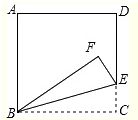 如图,将正方形纸片ABCD沿BE翻折,使点C落在点F处,若∠DEF=40°,则∠ABF的度数为50°.
如图,将正方形纸片ABCD沿BE翻折,使点C落在点F处,若∠DEF=40°,则∠ABF的度数为50°.
分析 根据翻折的性质可得∠BEF=∠BEC,∠EBF=∠EBC,然后求出∠BEC,再根据直角三角形两锐角互余求出∠EBC,然后根据∠ABF=90°-∠EBF-∠EBC代入数据进行计算即可得解.
解答  解:补全正方形如图,
解:补全正方形如图,
由翻折的性质得,∠BEF=∠BEC,∠EBF=∠EBC,
∵∠DEF=30°,
∴∠BEC=$\frac{1}{2}$(180°-∠DEF)=$\frac{1}{2}$(180°-40°)=70°,
∴∠EBC=90°-∠BEC=90°-70°=20°,
∴∠ABF=90°-∠EBF-∠EBC
=90°-20°-20°
=50°.
故答案为:50°.
点评 本题考查了翻折变换的性质,正方形的性质,熟记翻折变换前后的图形能够重合是解题的关键,难点在于作辅助线补全正方形.

练习册系列答案
相关题目
12.把分式$\frac{y}{x+3y}$中的x和y都扩大3倍,分式的值( )
| A. | 扩大3倍 | B. | 扩大9倍 | C. | 不变 | D. | 缩小3倍 |
13.已知圆O的半径为5,弦AB=8,D为弦AB上一点,且AD=1,过点D作CD⊥AB,交圆O于C,则CD长为( )
| A. | 1 | B. | 7 | C. | 8或1 | D. | 7或1 |
10.解分式方程$\frac{1}{x-1}+\frac{2x}{x+1}=2$时,在方程的两边同时乘以(x-1)(x+1),把原方程化为x+1+2x(x-1)=2(x-1)(x+1),这一变形过程体现的数学思想主要是( )
| A. | 类比思想 | B. | 转化思想 | C. | 方程思想 | D. | 函数思想 |
7. 有一种圆柱体茶叶筒如图所示,则它的俯视图是( )
有一种圆柱体茶叶筒如图所示,则它的俯视图是( )
 有一种圆柱体茶叶筒如图所示,则它的俯视图是( )
有一种圆柱体茶叶筒如图所示,则它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
11.已知点A(1,2)在反比例函数y=$\frac{k}{x}$的图象上,则该反比例函数的解析式是( )
| A. | y=$\frac{1}{x}$ | B. | y=$\frac{4}{x}$ | C. | y=$\frac{2}{x}$ | D. | y=2x |
 阅读与计算:请阅读以下材料,并完成相应的任务.
阅读与计算:请阅读以下材料,并完成相应的任务. 如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,且∠1=∠2.求证:AE=CF.
如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,且∠1=∠2.求证:AE=CF.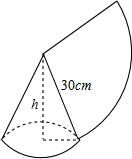 如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的高h等于20$\sqrt{2}$cm.
如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的高h等于20$\sqrt{2}$cm.