题目内容
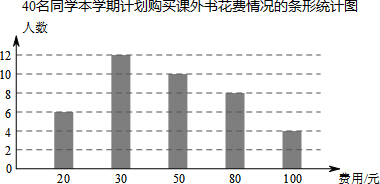
14. 如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,且∠1=∠2.求证:AE=CF.
如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,且∠1=∠2.求证:AE=CF.
分析 由平行四边形的性质得出AD=BC,AD∥BC,得出∠DAE=∠BCF,由邻补角关系和已知条件得出∠AED=∠CFB,由AAS证明△ADE≌△CBF,得出对应边相等即可.
解答 证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAE=∠BCF,
∵∠1+∠AED=180°,∠2+∠CFB=180°,∠1=∠2,
∴∠AED=∠CFB,
在△ADE和△CBF中,
$\left\{\begin{array}{l}{∠DAE=∠BCF}&{\;}\\{∠AED=∠CFB}&{\;}\\{AD=CB}&{\;}\end{array}\right.$,
∴△ADE≌△CBF(AAS),
∴AE=CF.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质、平行线的性质、邻补角关系;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
4.1-$\sqrt{15}$的值( )
| A. | 比-2大 | B. | 比-3大 | C. | 比-3小 | D. | 比-4小 |
5.下列运算正确的是( )
| A. | x2+x3=x6 | B. | 2x+3y=5xy | C. | (x3)2=x6 | D. | x6÷x3=x2 |
 如图,将正方形纸片ABCD沿BE翻折,使点C落在点F处,若∠DEF=40°,则∠ABF的度数为50°.
如图,将正方形纸片ABCD沿BE翻折,使点C落在点F处,若∠DEF=40°,则∠ABF的度数为50°. 某校为了发展校园足球运动,组建了校足球队,队员年龄分布如图所示,则这些队员年龄的众数是14.
某校为了发展校园足球运动,组建了校足球队,队员年龄分布如图所示,则这些队员年龄的众数是14.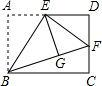 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,若AB=6,BC=4$\sqrt{6}$,则FD的长为4.
如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,若AB=6,BC=4$\sqrt{6}$,则FD的长为4.