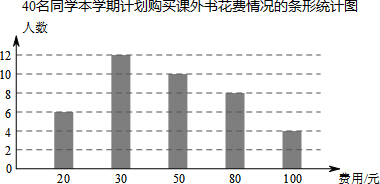
题目内容
13.已知圆O的半径为5,弦AB=8,D为弦AB上一点,且AD=1,过点D作CD⊥AB,交圆O于C,则CD长为( )| A. | 1 | B. | 7 | C. | 8或1 | D. | 7或1 |
分析 连接OB,OC1,过O作OE⊥CD,OF⊥AB,则四边形EDFO是矩形,根据矩形的性质得到OE=DF,OF=DE,根据勾股定理得到BF=$\sqrt{{5}^{2}-{4}^{2}}$=3,得到OE=DF=3,由勾股定理得到C1E=$\sqrt{{5}^{2}-{3}^{2}}$=4,于是得到结论.
解答 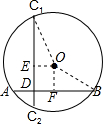 解:如图,
解:如图,
连接OB,OC1,过O作OE⊥CD,OF⊥AB,
则四边形EDFO是矩形,
∴OE=DF,OF=DE,
∵圆O的半径为5,弦AB=8,
∴AF=BF=4,
∴BF=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∵AD=1,∴DF=3,
∴OE=DF=3,
∴C1E=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴C2E=4,
∴C1D=7,C2D=1,
∴CD长为7或1,
故选D.
点评 本题考查了垂径定理,勾股定理的运用.关键是连接半径,将问题转化到直角三角形中,利用勾股定理,列方程求解.

练习册系列答案
相关题目
3.下列方程中是一元二次方程的是( )
| A. | x+2y=1 | B. | 2x(x-1)=2x2+3 | C. | x2-2=0 | D. | 3x+$\frac{1}{x}$=4 |
4.1-$\sqrt{15}$的值( )
| A. | 比-2大 | B. | 比-3大 | C. | 比-3小 | D. | 比-4小 |
1.若x>y,则下列变形正确的是( )
| A. | x+3>y+3 | B. | x-3<y-3 | C. | -3x>-3y | D. | -$\frac{x}{3}>-\frac{y}{3}$ |
8.下面说法正确的是( )
| A. | 1的绝对值是-1 | B. | 1的倒数是-1 | C. | 1的相反数是-1 | D. | 1的平方根是-1 |
5.下列运算正确的是( )
| A. | x2+x3=x6 | B. | 2x+3y=5xy | C. | (x3)2=x6 | D. | x6÷x3=x2 |
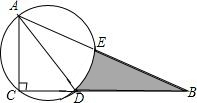 如图,已知△ABC,∠ACB=90°,∠B=30°,AD平分∠BAC,以AD为直径作圆O交AB于E,已知CD=2,则图中阴影部分的面积(用含x的代数式表示)为:2$\sqrt{3}$-$\frac{2}{3}$π.
如图,已知△ABC,∠ACB=90°,∠B=30°,AD平分∠BAC,以AD为直径作圆O交AB于E,已知CD=2,则图中阴影部分的面积(用含x的代数式表示)为:2$\sqrt{3}$-$\frac{2}{3}$π.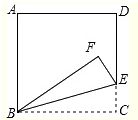 如图,将正方形纸片ABCD沿BE翻折,使点C落在点F处,若∠DEF=40°,则∠ABF的度数为50°.
如图,将正方形纸片ABCD沿BE翻折,使点C落在点F处,若∠DEF=40°,则∠ABF的度数为50°.