Question

14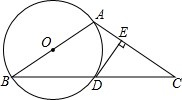．已知：如图，AB是⊙O的直径，AB=AC，交⊙O于点D，DE⊥AC，
求证：DE是⊙O的切线．

Answer 1

分析 连接OD，由等腰三角形的性质得出∠B=∠C，∠B=∠ODB，得出∠C=∠ODB，证出OD∥AC，再由已知条件证出DE⊥OD，即可得出DE是⊙O的切线．

解答 证明：连接OD，如图所示：
∵AB=AC，
∴∠B=∠C，
∵OB=OD，
∴∠B=∠ODB，
∴∠C=∠ODB，
∴OD∥AC，
∵DE⊥AC，
∴DE⊥OD，
∴DE是⊙O的切线．

点评 本题考查了切线的判定定理、等腰三角形的性质、平行线的判定与性质；熟练掌握切线的判定定理，由等腰三角形的性质得出角相等证出平行线是解决问题的关键．