题目内容
3.在△ABC中,AB>AC>BC,∠ACB=80°,点D、E在直线AB上,且AD=AC,BE=BC,求∠DCE的度数(直接写出答案)分析 分当点D、E在点A的同侧,当点D、E在点A的两侧时两种情况分类讨论后利用等腰三角形的性质即可求解.
解答  解:(1)当点D、E在点A的同侧,且都在AB上时,如图1,
解:(1)当点D、E在点A的同侧,且都在AB上时,如图1,
∵BE=BC,
∴∠BCE=(180°-∠ABC)÷2,
∵AD=AC,
∴∠ACD=(180°-∠BAC)÷2,
∵∠DCE=∠BCE+∠ACD-∠ACB,
∴∠DCE=(180°-∠ABC)÷2+(∠180°-∠BAC)÷2-∠ACB
=(360°-∠ABC-∠BAC)÷2-∠ACB
=(180°+∠ACB)÷2-∠ACB
=90°-$\frac{1}{2}$∠ACB
=90°-$\frac{1}{2}$×80° =50°.
=50°.
(2)当点D、E在点A的两侧时,如图2,
∵BE=BC,
∴∠BEC=(180°-∠ABC)÷2,
∵AD=AC,
∴∠ADC=(180°-∠DAC)÷2=∠BAC÷2,
又∵∠DCE=∠BEC-∠ADC,
∴∠DCE=(∠180°-∠ABC)÷2-∠BAC÷2=(180°-∠ACB)÷2
=100°÷2=50°.
故∠DCE的度数为50°.
点评 本题考查了等腰三角形的性质,三角形外角的性质,三角形内角和定理等知识,体现了分类讨论的数学思想,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
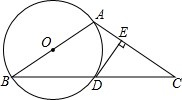 已知:如图,AB是⊙O的直径,AB=AC,交⊙O于点D,DE⊥AC,
已知:如图,AB是⊙O的直径,AB=AC,交⊙O于点D,DE⊥AC,