题目内容
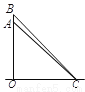
如图,一枚运载火箭从地面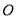 处发射,当火箭到达
处发射,当火箭到达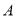 点时,从地面
点时,从地面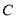 处的雷达站测得
处的雷达站测得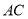 的距离是
的距离是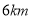 ,仰角是
,仰角是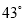 ,
,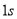 后,火箭到达
后,火箭到达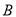 点,此时测得
点,此时测得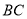 的距离是
的距离是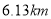 ,仰角为
,仰角为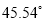 ,这枚火箭从
,这枚火箭从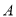 点到
点到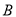 点的平均速度是多少?(精确到
点的平均速度是多少?(精确到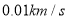 )
)
 这枚火箭从点到点的平均速度是
【解析】试题分析:首先根据Rt△BCO中∠BCO的正弦值得出OB的长度,然后根据Rt△ACO中∠ACO的正弦值得出OA的长度,从而得出答案.
试题解析:在Rt中,
∴
在Rt中, ∴
∴
答:这枚火箭从点到点的平均速度是.
这枚火箭从点到点的平均速度是
【解析】试题分析:首先根据Rt△BCO中∠BCO的正弦值得出OB的长度,然后根据Rt△ACO中∠ACO的正弦值得出OA的长度,从而得出答案.
试题解析:在Rt中,
∴
在Rt中, ∴
∴
答:这枚火箭从点到点的平均速度是.
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
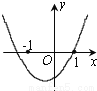
欣语文化快乐暑假沈阳出版社系列答案已知函数y=(x-a)(x-b)(其中a>b)的图象如图所示,则函数y=ax+b的图象可能正确的是( )
A. 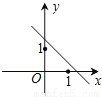 B.
B. 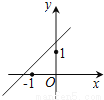 C.
C. 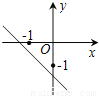 D.
D. 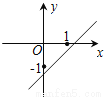
 D
【解析】根据图象可得出方程(x-a)(x-b)=0的两个实数根为a,b,且一正一负,负数的绝对值大,
∵a>b,∴a>0,b<0,
∴函数y=ax+b的图象经过第一、三、四象限,
故选:D.
D
【解析】根据图象可得出方程(x-a)(x-b)=0的两个实数根为a,b,且一正一负,负数的绝对值大,
∵a>b,∴a>0,b<0,
∴函数y=ax+b的图象经过第一、三、四象限,
故选:D. 如图,Rt△ABC中,∠C =90°,∠ABC的平分线BD交AC于D,若AD =5cm,CD =3cm,则点D到AB的距离DE是( )
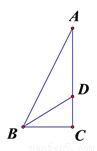
A. 5cm B. 4cm C. 3cm D. 2cm
 C
【解析】∵点D到AB的距离是DE ,
∴DE⊥AB,
∵BD平分∠ABC,∠C =90°,
∴把Rt△BDC沿BD翻折后,点C在线段AB上的点E处,
∴DE=CD,
∵CD =3cm,
∴DE=3cm.
故选:C.
C
【解析】∵点D到AB的距离是DE ,
∴DE⊥AB,
∵BD平分∠ABC,∠C =90°,
∴把Rt△BDC沿BD翻折后,点C在线段AB上的点E处,
∴DE=CD,
∵CD =3cm,
∴DE=3cm.
故选:C. 如图,四边形ABCD沿直线l对折后互相重合,如果AD∥BC,那么△ABC___(填“是”或“不是”)等腰三角形.
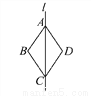
 是
【解析】试题分析:根据折叠图形的性质可知:∠BAC=∠DAC,根据平行线的性质可知:∠DAC=∠ACB,则∠BAC=∠ACB,即△ABC为等腰三角形.
是
【解析】试题分析:根据折叠图形的性质可知:∠BAC=∠DAC,根据平行线的性质可知:∠DAC=∠ACB,则∠BAC=∠ACB,即△ABC为等腰三角形. 如图所示,A,B两地之间有一座山,汽车原来从A地到B地需要经C地沿折线A—C—B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10 km,∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1 km,参考数据: 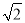 ≈1.41,
≈1.41, 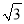 ≈1.73)
≈1.73)
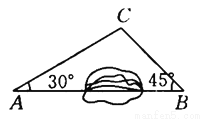
 隧道开通后,汽车从A地到B地比原来少走约3.4 km
【解析】试题分析:过点C作AB的垂线CD,垂足为D,在直角△ACD和直角△CBD中,解直角三角形求出CD,AD,BC,就可以得到结论.
试题解析:过点C作AB的垂线CD,垂足为D.
∵AC=10km,∠A=30°,
∴CD=AC=5(km).
AD==5(km).
在Rt△CDB中,
∵∠B=45°,
...
隧道开通后,汽车从A地到B地比原来少走约3.4 km
【解析】试题分析:过点C作AB的垂线CD,垂足为D,在直角△ACD和直角△CBD中,解直角三角形求出CD,AD,BC,就可以得到结论.
试题解析:过点C作AB的垂线CD,垂足为D.
∵AC=10km,∠A=30°,
∴CD=AC=5(km).
AD==5(km).
在Rt△CDB中,
∵∠B=45°,
... 如图,在高度是21米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD=_________米(结果保留根号).
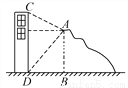
 (7++21)
【解析】试题分析:作AE⊥CD于点E.在Rt△ABD中,∠ADB=45°,∴DE=AE=BD=AB=21(米),
在Rt△AEC中,CE=AE•tan∠CAE=21×=7(米).则CD=(21+7)米.
(7++21)
【解析】试题分析:作AE⊥CD于点E.在Rt△ABD中,∠ADB=45°,∴DE=AE=BD=AB=21(米),
在Rt△AEC中,CE=AE•tan∠CAE=21×=7(米).则CD=(21+7)米. 已知:如图,直线y=3x+3与x轴交于C点,与y轴交于A点,B点在x轴上,△OAB是等腰直角三角形.
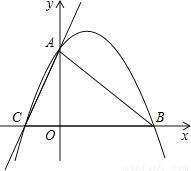
(1)求过A、B、C三点的抛物线的解析式;
(2)若P点是抛物线上的动点,且在第一象限,那么△PAB是否有最大面积?若有,求出此时P点的坐标和△PAB的最大面积;若没有,请说明理由.
 (1)y= -x2+2x+3(2)存在,()
【解析】试题分析:(1)求得直线y=3x+3与坐标轴的两交点坐标,然后根据OB=OA即可求得点B的坐标,然后利用待定系数法求得经过A、B、C三点的抛物线的解析式即可;
(2)首先利用待定系数法求得直线AB的解析式,然后根据CD∥AB得到两直线的k值相等,根据直线CD经过点C求得直线CD的解析式,然后求得直线CD和抛物线的交点坐标即可;
...
(1)y= -x2+2x+3(2)存在,()
【解析】试题分析:(1)求得直线y=3x+3与坐标轴的两交点坐标,然后根据OB=OA即可求得点B的坐标,然后利用待定系数法求得经过A、B、C三点的抛物线的解析式即可;
(2)首先利用待定系数法求得直线AB的解析式,然后根据CD∥AB得到两直线的k值相等,根据直线CD经过点C求得直线CD的解析式,然后求得直线CD和抛物线的交点坐标即可;
... 向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为y=ax2bx+c(a≠0).若此炮弹在第7秒与第14秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A. 第8秒 B. 第10秒 C. 第12秒 D. 第15秒
 B
【解析】试题分析:炮弹在第7秒与第14秒时的高度相等所以抛物线的对称轴是在第10秒处,所以在第10秒处高度是最高的.
故选B.
B
【解析】试题分析:炮弹在第7秒与第14秒时的高度相等所以抛物线的对称轴是在第10秒处,所以在第10秒处高度是最高的.
故选B. 已知下列函数:①y=x2;②y=-x2;③y=(x-1)2+2.其中图象通过平移可以得到函数y=x2+2x-3的图象的有_____________(填写所有正确选项的序号).
 ①③
【解析】把函数y=x2+2x-3整理成顶点式解析式y=(x+1)2-4,得到y=x2+2x-3的顶点坐标为(-1,-4),然后根据顶点的变化确定出:
①y=x2向左平移1个单位,向下4个单位,得到y=x2+2x-3;
②y=x2不能平移得到y=x2+2x-3;
③y=(x-1)2+2向左平移2个单位,向下平移6个单位得到y=x2+2x-3,
所以,①③图象通过平移可以得到函...
①③
【解析】把函数y=x2+2x-3整理成顶点式解析式y=(x+1)2-4,得到y=x2+2x-3的顶点坐标为(-1,-4),然后根据顶点的变化确定出:
①y=x2向左平移1个单位,向下4个单位,得到y=x2+2x-3;
②y=x2不能平移得到y=x2+2x-3;
③y=(x-1)2+2向左平移2个单位,向下平移6个单位得到y=x2+2x-3,
所以,①③图象通过平移可以得到函... 
