ĢāÄæÄŚČŻ
ČēĶ¼£¬Rt”÷ABCÖŠ£¬”ĻC =90”ć£¬”ĻABCµÄĘ½·ÖĻßBD½»ACÓŚD£¬ČōAD =5cm£¬CD =3cm£¬ŌņµćDµ½ABµÄ¾ąĄėDEŹĒ£Ø £©
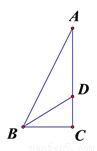
A. 5cm B. 4cm C. 3cm D. 2cm
 C
”¾½āĪö”æ”ßµćDµ½ABµÄ¾ąĄėŹĒDE £¬
”ąDE”ĶAB£¬
”ßBDĘ½·Ö”ĻABC£¬”ĻC =90”ć£¬
”ą°ŃRt”÷BDCŃŲBD·ÕŪŗ󣬵ćCŌŚĻ߶ĪABÉĻµÄµćE“¦£¬
”ąDE=CD£¬
”ßCD =3cm£¬
”ąDE=3cm.
¹ŹŃ”£ŗC.
C
”¾½āĪö”æ”ßµćDµ½ABµÄ¾ąĄėŹĒDE £¬
”ąDE”ĶAB£¬
”ßBDĘ½·Ö”ĻABC£¬”ĻC =90”ć£¬
”ą°ŃRt”÷BDCŃŲBD·ÕŪŗ󣬵ćCŌŚĻ߶ĪABÉĻµÄµćE“¦£¬
”ąDE=CD£¬
”ßCD =3cm£¬
”ąDE=3cm.
¹ŹŃ”£ŗC.
½«µćA£Ø©2£¬©3£©ĻņÓŅĘ½ŅĘ3øöµ„Ī»³¤¶ČµĆµ½µćB£¬ŌņµćBĖł“¦µÄĻóĻŽŹĒ
A. µŚŅ»ĻóĻŽ B. µŚ¶žĻóĻŽ C. µŚČżĻóĻŽ D. µŚĖÄĻóĻŽ
 D
”¾½āĪö”æµćA(£2£¬£3)ĻņÓŅĘ½ŅĘ3øöµ„Ī»³¤¶ČĖłµĆµ½µÄµćBµÄ×ų±źĪŖ(1£¬£3)£¬¹ŹµćBŌŚµŚĖÄĻóĻŽ£®
D
”¾½āĪö”æµćA(£2£¬£3)ĻņÓŅĘ½ŅĘ3øöµ„Ī»³¤¶ČĖłµĆµ½µÄµćBµÄ×ų±źĪŖ(1£¬£3)£¬¹ŹµćBŌŚµŚĖÄĻóĻŽ£® ŅņŹ½·Ö”¾½āĪö”æ
£Ø1£©20a3©30a2
£Ø2£©16©£Ø2a+3b£©2
£Ø3£©©16x2y2+12xy3z
£Ø4£©5x2y©25x2y2+40x3y
£Ø5£©x2£Øa©b£©2©y2£Øb©a£©2
£Ø6£©£Øa2+b2£©2©4a2b2
£Ø7£©18b£Øa©b£©2+12£Øb©a£©3
£Ø8£©x£Øx2+1£©2©4x3
£Ø9£©£Øx2©2x£©2©3£Øx2©2x£©
£Ø10£©£Ø2x©1£©2©6£Ø2x©1£©+9
£Ø11£©16x4©72x2y2+81y4
£Ø12£©a5©a
£Ø13£©25£Øx+y£©2©9£Øx©y£©2
£Ø14£©m2©3m©28
£Ø15£©x2+x©20£®
 £Ø1£©10a2£Ø2a©3£©£»£Ø2£©£Ø4+2a+3b£©£Ø4©2a©3b£©£»
£Ø3£©©4xy2£Ø4x©3yz£©£»
£Ø4£©5x2y£Ø1©5y+8x£©£»
£Ø5£©£Øa©b£©2£Øx+y£©£Øx©y£©£»
£Ø6£©£Øa+b£©2£Øa©b£©2£»
£Ø7£©6£Øb©a£©2£Ø5b©2a£©£»
£Ø8£©x£Øx+1£©2£Øx©1£©2£»
£Ø9£©x£Øx©2£©£Øx©3£©£Øx+1£©£»
£Ø10£©4£Øx...
£Ø1£©10a2£Ø2a©3£©£»£Ø2£©£Ø4+2a+3b£©£Ø4©2a©3b£©£»
£Ø3£©©4xy2£Ø4x©3yz£©£»
£Ø4£©5x2y£Ø1©5y+8x£©£»
£Ø5£©£Øa©b£©2£Øx+y£©£Øx©y£©£»
£Ø6£©£Øa+b£©2£Øa©b£©2£»
£Ø7£©6£Øb©a£©2£Ø5b©2a£©£»
£Ø8£©x£Øx+1£©2£Øx©1£©2£»
£Ø9£©x£Øx©2£©£Øx©3£©£Øx+1£©£»
£Ø10£©4£Øx... Ō²”¢³¤·½ŠĪ”¢Õż·½ŠĪ¶¼ŹĒÖį¶Ō³ĘĶ¼ŠĪ£¬Ėµ³öĖūĆĒ·Ö±šÓŠ¼øĢõ¶Ō³ĘÖį.
 Ō²”¢³¤·½ŠĪ”¢Õż·½ŠĪµÄ¶Ō³ĘÖįµÄŹżĮæ·Ö±šŹĒĪŽŹżĢõ”¢2Ģõ”¢4Ģõ
”¾½āĪö”æŹŌĢā·ÖĪö£ŗŅĄ¾ŻÖį¶Ō³ĘĶ¼ŠĪµÄøÅÄī£¬¼“ŌŚĘ½ĆęÄŚ£¬Čē¹ūŅ»øöĶ¼ŠĪŃŲŅ»ĢõÖ±ĻßÕŪµž£¬Ö±ĻßĮ½ÅŌµÄ²æ·ÖÄܹ»ĶźČ«ÖŲŗĻ£¬ÕāŃłµÄĶ¼ŠĪ½Š×öÖį¶Ō³ĘĶ¼ŠĪ£¬ÕāĢõÖ±Ļß¾ĶŹĒÕāøöÖį¶Ō³ĘĶ¼ŠĪµÄ¶Ō³ĘÖį£¬¾Ż“Ė¼“æɽā“š£®
ŹŌĢā½āĪö£ŗ”߶ŌÓŚŌ²Ą“Ėµ£¬¹żŌ²ŠÄµÄČĪŅāŅ»ĢõÖ±Ļߣ¬¶¼Äܹ»½«ÕāøöŌ²·Ö³ÉÄܹ»»„ĻąÖŲŗĻµÄĮ½²æ·Ö
”ą¹żŌ²ŠÄµÄÖ±Ļߣ¬¶¼ŹĒŌ²µÄ¶Ō³ĘÖį£¬
”ąŌ²ÓŠĪŽŹżĢõ...
Ō²”¢³¤·½ŠĪ”¢Õż·½ŠĪµÄ¶Ō³ĘÖįµÄŹżĮæ·Ö±šŹĒĪŽŹżĢõ”¢2Ģõ”¢4Ģõ
”¾½āĪö”æŹŌĢā·ÖĪö£ŗŅĄ¾ŻÖį¶Ō³ĘĶ¼ŠĪµÄøÅÄī£¬¼“ŌŚĘ½ĆęÄŚ£¬Čē¹ūŅ»øöĶ¼ŠĪŃŲŅ»ĢõÖ±ĻßÕŪµž£¬Ö±ĻßĮ½ÅŌµÄ²æ·ÖÄܹ»ĶźČ«ÖŲŗĻ£¬ÕāŃłµÄĶ¼ŠĪ½Š×öÖį¶Ō³ĘĶ¼ŠĪ£¬ÕāĢõÖ±Ļß¾ĶŹĒÕāøöÖį¶Ō³ĘĶ¼ŠĪµÄ¶Ō³ĘÖį£¬¾Ż“Ė¼“æɽā“š£®
ŹŌĢā½āĪö£ŗ”߶ŌÓŚŌ²Ą“Ėµ£¬¹żŌ²ŠÄµÄČĪŅāŅ»ĢõÖ±Ļߣ¬¶¼Äܹ»½«ÕāøöŌ²·Ö³ÉÄܹ»»„ĻąÖŲŗĻµÄĮ½²æ·Ö
”ą¹żŌ²ŠÄµÄÖ±Ļߣ¬¶¼ŹĒŌ²µÄ¶Ō³ĘÖį£¬
”ąŌ²ÓŠĪŽŹżĢõ... µČŃüČż½ĒŠĪµÄ¶Ō³ĘÖįŹĒ______£®
 ¶„½ĒĘ½·ÖĻßĖłŌŚÖ±Ļß
”¾½āĪö”æŅ»øöĶ¼ŠĪŃŲŅ»ĢõÖ±Ļ߶ŌÕŪ£¬Ö±ĻßĮ½ÅŌµÄ²æ·ÖÄܹ»ĶźČ«ÖŲŗĻ£¬ÄĒĆ“ÕāøöĶ¼ŠĪ¾ĶŹĒÖį¶Ō³ĘĶ¼ŠĪ£¬ÕāĢõÖ±Ļß¾ĶŹĒÕāøöĶ¼ŠĪµÄŅ»Ģõ¶Ō³ĘÖį,ČēĶ¼ĖłŹ¾£ŗµČŃüČż½ĒŠĪµÄ¶Ō³ĘÖįŹĒ¶„½ĒĘ½·ÖĻßĖłŌŚÖ±Ļß.
¹Ź“š°øŹĒ£ŗ¶„½ĒĘ½·ÖĻßĖłŌŚÖ±Ļß.
¶„½ĒĘ½·ÖĻßĖłŌŚÖ±Ļß
”¾½āĪö”æŅ»øöĶ¼ŠĪŃŲŅ»ĢõÖ±Ļ߶ŌÕŪ£¬Ö±ĻßĮ½ÅŌµÄ²æ·ÖÄܹ»ĶźČ«ÖŲŗĻ£¬ÄĒĆ“ÕāøöĶ¼ŠĪ¾ĶŹĒÖį¶Ō³ĘĶ¼ŠĪ£¬ÕāĢõÖ±Ļß¾ĶŹĒÕāøöĶ¼ŠĪµÄŅ»Ģõ¶Ō³ĘÖį,ČēĶ¼ĖłŹ¾£ŗµČŃüČż½ĒŠĪµÄ¶Ō³ĘÖįŹĒ¶„½ĒĘ½·ÖĻßĖłŌŚÖ±Ļß.
¹Ź“š°øŹĒ£ŗ¶„½ĒĘ½·ÖĻßĖłŌŚÖ±Ļß. ½Ē”¢Ļ߶Ī”¢Čż½ĒŠĪ”¢Ō²”¢³¤·½ŠĪŗĶÕż·½ŠĪÖŠ£¬Ņ»¶ØŹĒÖį¶Ō³ĘĶ¼ŠĪµÄÓŠ£Ø £©
A. 4øö B. 5øö C. 6øö D. 3øö
 B
”¾½āĪö”æĶعż·ÖĪöæÉÖŖ£¬½Ē”¢Ļ߶Ī”¢Ō²”¢³¤·½ŠĪŗĶÕż·½ŠĪ¶¼ŹĒÖį¶Ō³ĘĶ¼ŠĪ£¬
¹ŹŃ”£ŗB.
B
”¾½āĪö”æĶعż·ÖĪöæÉÖŖ£¬½Ē”¢Ļ߶Ī”¢Ō²”¢³¤·½ŠĪŗĶÕż·½ŠĪ¶¼ŹĒÖį¶Ō³ĘĶ¼ŠĪ£¬
¹ŹŃ”£ŗB. ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻB”Ł”ĻC.ĒóÖ¤£ŗAB”ŁAC.
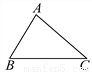
 ¼ū½āĪö
”¾½āĪö”æŹŌĢā·ÖĪö£ŗŹ×ĻČ¼ŁÉčAB=AC£¬“Ó¶ųµĆ³öÓėŅŃÖŖĢõ¼žĆ¬¶Ü£¬“Ó¶ųµĆ³ö“š°ø£®
ŹŌĢā½āĪö£ŗ¼ŁÉčAB=AC£¬ Ōņ”ĻB=”ĻC£¬”ąÓėŅŃÖŖƬ¶Ü£¬”ąAB”ŁAC£®
¼ū½āĪö
”¾½āĪö”æŹŌĢā·ÖĪö£ŗŹ×ĻČ¼ŁÉčAB=AC£¬“Ó¶ųµĆ³öÓėŅŃÖŖĢõ¼žĆ¬¶Ü£¬“Ó¶ųµĆ³ö“š°ø£®
ŹŌĢā½āĪö£ŗ¼ŁÉčAB=AC£¬ Ōņ”ĻB=”ĻC£¬”ąÓėŅŃÖŖƬ¶Ü£¬”ąAB”ŁAC£® ČēĶ¼,Ņ»Ć¶ŌĖŌŲ»š¼ż“ÓµŲĆę “¦·¢Éä,µ±»š¼żµ½“ļ
“¦·¢Éä,µ±»š¼żµ½“ļ µćŹ±,“ÓµŲĆę
µćŹ±,“ÓµŲĆę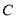 “¦µÄĄ×“ļÕ¾²āµĆ
“¦µÄĄ×“ļÕ¾²āµĆ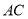 µÄ¾ąĄėŹĒ
µÄ¾ąĄėŹĒ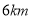 ,Ńö½ĒŹĒ
,Ńö½ĒŹĒ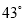 ,
,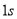 ŗó,»š¼żµ½“ļ
ŗó,»š¼żµ½“ļ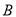 µć,“ĖŹ±²āµĆ
µć,“ĖŹ±²āµĆ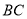 µÄ¾ąĄėŹĒ
µÄ¾ąĄėŹĒ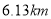 ,Ńö½ĒĪŖ
,Ńö½ĒĪŖ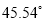 ,Õāƶ»š¼ż“Ó
,Õāƶ»š¼ż“Ó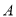 µćµ½
µćµ½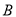 µćµÄĘ½¾łĖŁ¶ČŹĒ¶ąÉŁ?(¾«Č·µ½
µćµÄĘ½¾łĖŁ¶ČŹĒ¶ąÉŁ?(¾«Č·µ½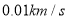 )
)
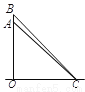
 Õāƶ»š¼ż“Óµćµ½µćµÄĘ½¾łĖŁ¶ČŹĒ
”¾½āĪö”æŹŌĢā·ÖĪö£ŗŹ×ĻČøł¾ŻRt”÷BCOÖŠ”ĻBCOµÄÕżĻŅÖµµĆ³öOBµÄ³¤¶Č£¬Č»ŗóøł¾ŻRt”÷ACOÖŠ”ĻACOµÄÕżĻŅÖµµĆ³öOAµÄ³¤¶Č£¬“Ó¶ųµĆ³ö“š°ø£®
ŹŌĢā½āĪö£ŗŌŚRtÖŠ,
”ą
ŌŚRtÖŠ, ”ą
”ą
“š:Õāƶ»š¼ż“Óµćµ½µćµÄĘ½¾łĖŁ¶ČŹĒ.
Õāƶ»š¼ż“Óµćµ½µćµÄĘ½¾łĖŁ¶ČŹĒ
”¾½āĪö”æŹŌĢā·ÖĪö£ŗŹ×ĻČøł¾ŻRt”÷BCOÖŠ”ĻBCOµÄÕżĻŅÖµµĆ³öOBµÄ³¤¶Č£¬Č»ŗóøł¾ŻRt”÷ACOÖŠ”ĻACOµÄÕżĻŅÖµµĆ³öOAµÄ³¤¶Č£¬“Ó¶ųµĆ³ö“š°ø£®
ŹŌĢā½āĪö£ŗŌŚRtÖŠ,
”ą
ŌŚRtÖŠ, ”ą
”ą
“š:Õāƶ»š¼ż“Óµćµ½µćµÄĘ½¾łĖŁ¶ČŹĒ. ČēĶ¼£¬ŅŃÖŖÅ×ĪļĻßy=-x2+bx+cÓėxÖįµÄĮ½øö½»µć·Ö±šĪŖA(x1£¬0)£¬B(x2£¬0) £¬ ĒŅx1+x2=4£¬  .
.
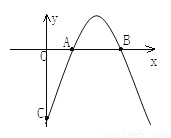
(1)ĒóÅ×ĪļĻߵēśŹż±ķ“ļŹ½;
(2)ÉčÅ×ĪļĻßÓėyÖį½»ÓŚCµć£¬ĒóÖ±ĻßBCµÄ±ķ“ļŹ½;
(3)Ēó”÷ABCµÄĆ껿.
 £Ø1£©øĆÅ×ĪļĻߵēśŹż±ķ“ļŹ½ĪŖy=-x2+4x-3£»£Ø2£©Ö±ĻßBCµÄ“śŹż±ķ“ļŹ½ĪŖy=x-3£»£Ø3£©S”÷ABC=3.
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ĻČ½ā·½³Ģ×é, ĒóµĆx1”¢x2µÄÖµ£¬ŌŁ“śČėÅ×ĪļĻßy=-x2+bx+c¼“æÉĒóµĆÅ×ĪļĻߵēśŹż±ķ“ļŹ½£»
£Ø2£©ÉčÖ±ĻßBCµÄ±ķ“ļŹ½ĪŖy=kx+m£¬ĻČĒóµĆÅ×ĪļĻßÓėyÖįµÄ½»µć×ų±ź£¬ŌŁøł¾Ż“ż¶ØĻµŹż·Ø¼“æÉĒóµĆÖ±ĻßBCµÄ±ķ“ļŹ½£»
£Ø3£©·Ö±šĒó³öAB”¢OCµÄ³¤£¬ŌŁøł...
£Ø1£©øĆÅ×ĪļĻߵēśŹż±ķ“ļŹ½ĪŖy=-x2+4x-3£»£Ø2£©Ö±ĻßBCµÄ“śŹż±ķ“ļŹ½ĪŖy=x-3£»£Ø3£©S”÷ABC=3.
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ĻČ½ā·½³Ģ×é, ĒóµĆx1”¢x2µÄÖµ£¬ŌŁ“śČėÅ×ĪļĻßy=-x2+bx+c¼“æÉĒóµĆÅ×ĪļĻߵēśŹż±ķ“ļŹ½£»
£Ø2£©ÉčÖ±ĻßBCµÄ±ķ“ļŹ½ĪŖy=kx+m£¬ĻČĒóµĆÅ×ĪļĻßÓėyÖįµÄ½»µć×ų±ź£¬ŌŁøł¾Ż“ż¶ØĻµŹż·Ø¼“æÉĒóµĆÖ±ĻßBCµÄ±ķ“ļŹ½£»
£Ø3£©·Ö±šĒó³öAB”¢OCµÄ³¤£¬ŌŁøł... 
