题目内容
学校合唱一队的人数是合唱二队人数的
少10人,如果从合唱二队调20人到合唱一队,那么两队人数恰好相同,求两队原有的人数.
| 4 |
| 5 |
考点:一元一次方程的应用
专题:
分析:设合唱二队的人数是x人,则合唱一队人数(
x-10)人.根据等量关系“从合唱二队调20人到合唱一队,那么两队人数恰好相同”列出方程.
| 4 |
| 5 |
解答:解:设合唱二队的人数是x人,则合唱一队人数(
x-10)人.则
x-20=(
x-10)+20,
整理,得
5x-100=4x+50,
解得 x=150.
则
x-10=
×150-10=110.
答:合唱一原有的人数是110人,合唱二队原有人数是150人.
| 4 |
| 5 |
x-20=(
| 4 |
| 5 |
整理,得
5x-100=4x+50,
解得 x=150.
则
| 4 |
| 5 |
| 4 |
| 5 |
答:合唱一原有的人数是110人,合唱二队原有人数是150人.
点评:本题考查了一元一次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
 已知:如图,CE平分∠ACD,∠1=∠2.求证:AB∥CD
已知:如图,CE平分∠ACD,∠1=∠2.求证:AB∥CD 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF= 如图,在平面直角坐标系中,直线y=
如图,在平面直角坐标系中,直线y=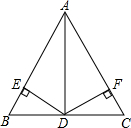 如图,在△ABC中,AB=5,AD=4,BD=DC=3,且DE⊥AB于E,DF⊥AC于点F.
如图,在△ABC中,AB=5,AD=4,BD=DC=3,且DE⊥AB于E,DF⊥AC于点F. a,b,c三个数在数轴上的位置如图,化简|a-b|-|a+c|+|c-b|=
a,b,c三个数在数轴上的位置如图,化简|a-b|-|a+c|+|c-b|=