题目内容
 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=| 1 |
| 2 |
(1)求证:BE=CE;
(2)求证:直线BF是⊙O的切线;
(3)若AB=10,sin∠CBF=
| ||
| 5 |
考点:切线的判定,等腰三角形的性质,勾股定理,扇形面积的计算,锐角三角函数的定义
专题:综合题
分析:(1)由AB是⊙O的直径可得AE⊥BC,然后根据等腰三角形的性质就可证到BE=CE.
(2)由等腰三角形的性质可得∠BAE=
∠CAB,从而得到∠BAE=∠CBF,进而可以证到∠ABF=90°,就可得到直线BF是⊙O的切线.
(3)利用三角函数可求出BE的长,再根据勾股定理可求出AE的长,然后用半圆OAB的面积减去△AEB的面积就可得到阴影部分的面积.
(2)由等腰三角形的性质可得∠BAE=
| 1 |
| 2 |
(3)利用三角函数可求出BE的长,再根据勾股定理可求出AE的长,然后用半圆OAB的面积减去△AEB的面积就可得到阴影部分的面积.
解答:(1)证明:∵AB是⊙O的直径,
∴∠AEB=90°,即AE⊥BC.
∵AB=AC,
∴BE=CE.
(2)证明:∵AB=AC,AE⊥BC,
∴∠BAE+∠ABE=90°,∠BAE=
∠CAB.
∵∠CBF=
∠CAB,
∴∠BAE=∠CBF.
∴∠CBF+∠ABE=90°,即∠ABF=90°.
∵AB是⊙O的直径,
∴直线BF是⊙O的切线.
(3)解:∵sin∠CBF=
,∠BAE=∠CBF,
∴sin∠BAE=
.
∵∠AEB=90°,AB=10,
∴BE=AB•sin∠BAE=10×
=2
.
∵∠AEB=90°,
∴AE=
=4
.
∴S阴影=S半圆A0B-S△ABE=
π(
)2-
AE•BE=
π(
)2-
×2
×4
=
-20.
∴阴影部分的面积为
-20.
∴∠AEB=90°,即AE⊥BC.
∵AB=AC,
∴BE=CE.
(2)证明:∵AB=AC,AE⊥BC,
∴∠BAE+∠ABE=90°,∠BAE=
| 1 |
| 2 |
∵∠CBF=
| 1 |
| 2 |
∴∠BAE=∠CBF.

∴∠CBF+∠ABE=90°,即∠ABF=90°.
∵AB是⊙O的直径,
∴直线BF是⊙O的切线.
(3)解:∵sin∠CBF=
| ||
| 5 |
∴sin∠BAE=
| ||
| 5 |
∵∠AEB=90°,AB=10,
∴BE=AB•sin∠BAE=10×
| ||
| 5 |
| 5 |
∵∠AEB=90°,
∴AE=
| AB2-BE2 |
| 5 |
∴S阴影=S半圆A0B-S△ABE=
| 1 |
| 2 |
| AB |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
| 25π |
| 2 |
∴阴影部分的面积为
| 25π |
| 2 |
点评:本题考查了切线的判定、直径所对的圆周角、等腰三角形的性质、三角函数的定义、勾股定理、扇形的面积等知识,有一定的综合性.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
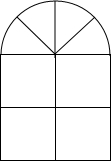 如图,一个窗户的上部是由四个扇形组成的一个半径为R的半圆,下部是边长相同的四个小正方形.
如图,一个窗户的上部是由四个扇形组成的一个半径为R的半圆,下部是边长相同的四个小正方形. 给出如图.
给出如图. 如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:
如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求: 如图,正方形ABCD的边长为a,点E、F分别在边BC、CD上,且∠EAF=45°,求△CEF的周长.
如图,正方形ABCD的边长为a,点E、F分别在边BC、CD上,且∠EAF=45°,求△CEF的周长.