��Ŀ����
�Ƚ�����ÿС����������ʽ����Ĵ�С(�ں����������������������)��
��32��42 2��3��4����22��22 2��2��2����12��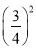 2��1��
2��1��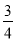 ��
��
��(��2) 2��52 2��(��2)��5����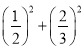
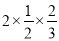
ͨ���۲��������ʽ����������ĸ����ʾ������ʽ�з�ӳ��һ����ɣ�
 (1������2������3������4������5������ ��2ab����a��bʱȡ�Ⱥţ���
������������������ֱ�����������ij˷��������������ֵ���ٸ����������Ƚϴ�С�ķ���Ƚϳ������Ĵ�С�����ܽ�����ɣ�
�����������1����32+42=25��2��3��4=24��
��32+42��2��3��4��
��2����22+22=8��2��2��2=8��
��22+22=2��2��2��
��3����12+()...
(1������2������3������4������5������ ��2ab����a��bʱȡ�Ⱥţ���
������������������ֱ�����������ij˷��������������ֵ���ٸ����������Ƚϴ�С�ķ���Ƚϳ������Ĵ�С�����ܽ�����ɣ�
�����������1����32+42=25��2��3��4=24��
��32+42��2��3��4��
��2����22+22=8��2��2��2=8��
��22+22=2��2��2��
��3����12+()...
��֪x2��3x��1=0����x��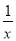 ��x2��
��x2��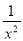 ��ֵ��
��ֵ��
 ��3,11
�����������������Ƚ�3x����,�ٷ�������ͬ����x�ó�����,������,��������ͬʱƽ���������.
���������
��Ϊ ,
���� ,
����ʽ������ͬʱ����x(x��0),
���� ,
,
,
��.�ʴ�Ϊ��-3��,11.
��3,11
�����������������Ƚ�3x����,�ٷ�������ͬ����x�ó�����,������,��������ͬʱƽ���������.
���������
��Ϊ ,
���� ,
����ʽ������ͬʱ����x(x��0),
���� ,
,
,
��.�ʴ�Ϊ��-3��,11. һ��������ε��ڽǺ�Ϊ540�㣬�����������ε�ÿһ����ǵ��ڣ� ��
A��108�� B��90�� C��72�� D��60��
 C��
��������
�����������˶����Ϊn���Σ���������ã�180��n��2��=540����ã�n=5�������������ε�ÿһ����ǵ��ڣ�360���5 =72�㣮��ѡC��
C��
��������
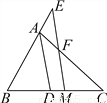
�����������˶����Ϊn���Σ���������ã�180��n��2��=540����ã�n=5�������������ε�ÿһ����ǵ��ڣ�360���5 =72�㣮��ѡC�� ��ͼ����֪��ABC��ADƽ�֡�BAC��BC�ڵ�D��BC���е�ΪM��ME��AD����BA���ӳ����ڵ�E����AC�ڵ�F.
(1)��֤��AE��AF��
(2)��֤��BE��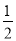 (AB��AC)��
(AB��AC)��
 ��1��֤������������2��֤��������.
�������������������1�����ݽ�ƽ���ߵ����ʼ�ƽ���ߵ������ס�AEF=��AFE�����ɵ�AE=AF����2����CG��EM����BA���ӳ�����G����֪AC=AG��������������λ�߶���������֤��BE=EG�������������ε���λ�߶�������֤�ý��ۣ�
���������
��1����DAƽ�֡�BAC��
���BAD=��CAD��
��AD��EM��
���BAD=...
��1��֤������������2��֤��������.
�������������������1�����ݽ�ƽ���ߵ����ʼ�ƽ���ߵ������ס�AEF=��AFE�����ɵ�AE=AF����2����CG��EM����BA���ӳ�����G����֪AC=AG��������������λ�߶���������֤��BE=EG�������������ε���λ�߶�������֤�ý��ۣ�
���������
��1����DAƽ�֡�BAC��
���BAD=��CAD��
��AD��EM��
���BAD=... ��ͼ���ڡ�ABC�У���ABC=90�㣬AB=8��BC=6����DE�ǡ�ABC����λ�ߣ��ӳ�DE����ABC����ǡ�ACM��ƽ�����ڵ�F�����߶�DF�ij�Ϊ���� ����
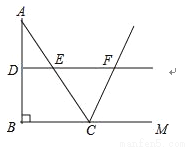
A. 7 B. 8 C. 9 D. 10
 B
�������������������RT��ABC�У��ߡ�ABC=90�㣬AB=8��BC=6����AC===10����DE�ǡ�ABC����λ�ߣ���DF��BM��DE=BC=3�����EFC=��FCM���ߡ�FCE=��FCM�����EFC=��ECF����EC=EF=AC=5����DF=DE+EF=3+5=8����ѡB��
B
�������������������RT��ABC�У��ߡ�ABC=90�㣬AB=8��BC=6����AC===10����DE�ǡ�ABC����λ�ߣ���DF��BM��DE=BC=3�����EFC=��FCM���ߡ�FCE=��FCM�����EFC=��ECF����EC=EF=AC=5����DF=DE+EF=3+5=8����ѡB�� y��3����x��4���ĺ��Ǹ����ò���ʽ��ʾΪ____________��
 3y��4x��0
��������������ã�y��3����ʾΪ3y��x��4����ʾΪ4x��
��y��3����x��4���ĺ��Ǹ�����
��3y+4x��0��
�ʴ�Ϊ��3y+4x��0��
3y��4x��0
��������������ã�y��3����ʾΪ3y��x��4����ʾΪ4x��
��y��3����x��4���ĺ��Ǹ�����
��3y+4x��0��
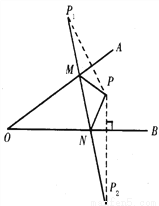
�ʴ�Ϊ��3y+4x��0�� ��ͼ,��AOB��һ��P,�ֱ�P����OA��OB�ĶԳƵ�P1��P2��P1P2��OA��M,��OB��N,��P1P2=5cm,���PMN���ܳ�Ϊ_______.
 5cm
����������P��P1,P��P2����OA��OB�Գƣ�
��PM=P1M,PN=P2N��
���PMN���ܳ�=P1P2��
���PMN���ܳ���5 cm.
5cm
����������P��P1,P��P2����OA��OB�Գƣ�
��PM=P1M,PN=P2N��
���PMN���ܳ�=P1P2��
���PMN���ܳ���5 cm. ��ͼ����֪��ABC�ǵȱ������Σ�D��E�ֱ��ڱ�BC��AC�ϣ���CD=CE������DE���ӳ�����F��ʹEF=AE������AF��BE��CF��
������������������������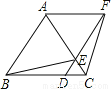
��1������ͼ���ҳ�һ��ȫ�������Σ��÷��š��ա���ʾ��������֤����
��2���ж��ı���ABDF���������ı��Σ���˵�����ɣ�
��3����AB=6��BD=2DC�����ı���ABEF�������.
 ��1������������2��ƽ���ı��Σ���3��
�������������������1����ͼ�ϼ���֪������������BDE�ա�FEC����BCE�ա�FDC����ABE�ա�ACF���ж�����������ȫ��ʱ�������бߵIJ��룬���Դ���Ĺؼ����ҳ���ȵıߣ�
��2���ɣ�1���Ľ�������֤��AB��DF��BD��AF������Ա߷ֱ�ƽ�е��ı�����ƽ���ı��Σ�
��3��EF��AB��EF��AB���ı���ABEF�����Σ�ֻҪ��������ε����...
��1������������2��ƽ���ı��Σ���3��
�������������������1����ͼ�ϼ���֪������������BDE�ա�FEC����BCE�ա�FDC����ABE�ա�ACF���ж�����������ȫ��ʱ�������бߵIJ��룬���Դ���Ĺؼ����ҳ���ȵıߣ�
��2���ɣ�1���Ľ�������֤��AB��DF��BD��AF������Ա߷ֱ�ƽ�е��ı�����ƽ���ı��Σ�
��3��EF��AB��EF��AB���ı���ABEF�����Σ�ֻҪ��������ε����...