题目内容
3.在平面直角坐标系中,点A(0,a)、B(b,0)且a>|b|.(1)若a、b满足a2+b2-4a-2b+5=0.
①求a、b的值;
②如图1,在①的条件下,将点B在x轴上平移,且b满足:0<b<2;在第一象限内以AB为斜边作等腰Rt△ABC,请用b表示S四边形AOBC,并写出解答过程.
(2)若将线段AB沿x轴向正方向移动a个单位得到线段DE(D对应A,E对应B)连接DO,作EF⊥DO于F,连接AF、BF.
①如图2,判断AF与BF的关系并说明理由;
②若BF=OA-OB,则∠OAF=60°(直接写出结果).
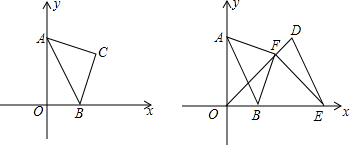
分析 (1)①化简得(a-2)2+(b-1)2=0,根据非负数的性质即可求出a、b.②利用S四边形AOBC=S△AOB+S△ABC即可解决.
(2)①结论:AF=FB,AF⊥FB,作FG⊥y轴,FH⊥x轴垂足分别为G、H,先证明四边形FHOG是正方形,然后证明△FGA≌△FHB得FA=FB,∠AFG=∠BFH所以∠AFB=∠GFH=90°.从而得证.
②由△FGA≌△FHB得∠FBH=∠OAF,在Rt△FBH中,求出cos∠FBH=$\frac{BH}{BF}$的值即可解决.
解答 解:(1)①∵a2+b2-4a-2b+5=0,
∴(a-2)2+(b-1)2=0,
∴a=2,b=1,
②∵A(0,2),B(b,0),
∴AB=$\sqrt{{b}^{2}+4}$,
∵△ABC是等腰直角三角形,
∴BC=$\frac{\sqrt{2}}{2}$AB=$\frac{\sqrt{2{b}^{2}+8}}{2}$,
∴S四边形AOBC=S△AOB+S△ABC=$\frac{1}{2}$•AO•BO+$\frac{1}{2}$BC2=$\frac{1}{4}$b2+b+1,(0<b<2).
(2)①结论:FA=FB,FA⊥FB,理由如下:
如图,作FG⊥y轴,FH⊥x轴垂足分别为G、H. ∵A(0,a)向右平移a个单位到D,
∵A(0,a)向右平移a个单位到D,
∴点D坐标为(a,a),点E坐标为(a+b,0),
∴∠DOE=45°,
∵EF⊥OD,
∴∠OFE=90°∠FOE=∠FEO=45°,
∴FO=EF,
∴FH=OH=HE=$\frac{1}{2}$(a+b),
∴点F坐标($\frac{a+b}{2}$,$\frac{a+b}{2}$),
∴FG=FH,四边形FHOG是正方形,
∴OG=FH=$\frac{a+b}{2}$,∠GFH=90°,
∴AG=AO-OG=a-$\frac{a+b}{2}$=$\frac{a-b}{2}$,BH=OH-OB=$\frac{a+b}{2}-b$=$\frac{a-b}{2}$,
∴AG=BH,
在△FGA和△FHB中,
$\left\{\begin{array}{l}{FG=FH}\\{∠FGA=∠FHB=90°}\\{AG=BH}\end{array}\right.$,
∴△FGA≌△FHB,
∴FA=FB,∠AFG=∠BFH,
∴∠AFB=∠GFH=90°.
AF⊥BF,AF=BF.
②∵△FGA≌△FHB,
∴∠FBH=∠OAF,
在Rt△BFH中,∵BF=OA-OB=a-b,BH=$\frac{a-b}{2}$,
∴cos∠FBH=$\frac{BH}{BF}$=$\frac{1}{2}$,
∴∠FBH=60°,
∴∠OAF=60°.
故答案为60°.
点评 本题考查全等三角形的判定和性质、勾股定理、非负数的性质、三角函数等知识,解题的关键是添加辅助线构造全等三角形,属于中考常考题型.

 名校课堂系列答案
名校课堂系列答案
 有一条公路连接A、B两地,一个骑行俱乐部上午9点从A地出发到达B地后返回,图中折线表示骑车人离A地的距离与时间的函数关系.有一辆客车9时从B地出发,以60千米/小时的速度为匀速行驶,图中的粗线表示客车离A地的距离与时间的函数关系.
有一条公路连接A、B两地,一个骑行俱乐部上午9点从A地出发到达B地后返回,图中折线表示骑车人离A地的距离与时间的函数关系.有一辆客车9时从B地出发,以60千米/小时的速度为匀速行驶,图中的粗线表示客车离A地的距离与时间的函数关系. 如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=3,以A为中心将腰AB顺时针旋转90°至AE,连接DE,若AB=5,CD=3,则BC的长为( )
如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=3,以A为中心将腰AB顺时针旋转90°至AE,连接DE,若AB=5,CD=3,则BC的长为( )