题目内容
15. 如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=3,以A为中心将腰AB顺时针旋转90°至AE,连接DE,若AB=5,CD=3,则BC的长为( )
如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=3,以A为中心将腰AB顺时针旋转90°至AE,连接DE,若AB=5,CD=3,则BC的长为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 首先过点A作AF⊥BC于点F,进而利用矩形的性质得出AF,FC的长,进而利用勾股定理得出答案.
解答  解:过点A作AF⊥BC于点F,
解:过点A作AF⊥BC于点F,
∵AD=DC=3,AD∥BC,
∴FC=AF=3,
又∵AB=5,
∴BF=4,
∴BC=4+3=7.
故选;C.
点评 此题主要考查了直角梯形的性质以及勾股定理、矩形的性质等知识,正确得出BF的长是解题关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
20. 如图是一枚六面体骰子的展开图,则掷一枚这样的骰子,朝上一面的数字是朝下一面的数字的3倍的概率是( )
如图是一枚六面体骰子的展开图,则掷一枚这样的骰子,朝上一面的数字是朝下一面的数字的3倍的概率是( )
 如图是一枚六面体骰子的展开图,则掷一枚这样的骰子,朝上一面的数字是朝下一面的数字的3倍的概率是( )
如图是一枚六面体骰子的展开图,则掷一枚这样的骰子,朝上一面的数字是朝下一面的数字的3倍的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
7.下列几组数中,为勾股数的是( )
| A. | $\frac{3}{5}$,$\frac{4}{5}$,1 | B. | 3,4,6 | C. | 5,12,13 | D. | 0.9,1.2,1.5 |
5.为了解某小区居民的用水情况,随机抽查了10户家庭的月用水量,结果如表:
则关于这10户家庭的月用水量,下列说法错误的是( )
| 月用水量(吨) | 4 | 5 | 6 | 9 |
| 户数 | 3 | 4 | 2 | 1 |
| A. | 中位数是5 | B. | 极差是3 | C. | 平均数是5.3 | D. | 众数是5 |
 如图,已知AB=AC,B是AD中点,E是AB中点,求证:CD=2CE.
如图,已知AB=AC,B是AD中点,E是AB中点,求证:CD=2CE.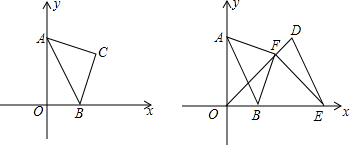
 如图,直线AB和CD相交于点0,则∠AOD=∠BOC.
如图,直线AB和CD相交于点0,则∠AOD=∠BOC.