题目内容
16．
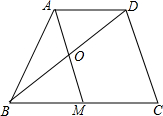如图，在四边形ABCD中，点M是边BC的中点，AD∥BC，AM∥DC，AM与BD交于点O．求证：AO=OM．
分析 连接DM，先证明四边形AMCD是平行四边形，得出AD=CM，由已知条件得出BM=CM，因此AD=BM，证出四边形ABMD是平行四边形，即可得出结论．
解答 证明：连接DM，如图所示：
∵AD∥BC，AM∥DC，
∴四边形AMCD是平行四边形，
∴AD=CM，
∵点M是边BC的中点，
∴BM=CM，
∴AD=BM，
又∵AD∥BC，
∴四边形ABMD是平行四边形，
∴AO=OM．
点评 本题考查了平行四边形的判定与性质；熟练掌握平行四边形的判定与性质，证明四边形ABMD是平行四边形是解决问题的关键．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
6．已知一次函数y=（m+1）x+m2-1（m为常数），若它的图象过原点，则（ ）
| A． | m=1 | B． | m=±1 | C． | m=-1 | D． | m=0 |
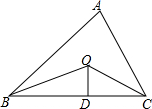如图，已知△ABC的周长是22，OB、OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD=3，△ABC的面积是多少？
如图，⊙O是△ABC的内切圆，⊙O切BC于点D，BD=3，CD=2，△ABC的周长为14，则AB=5．
11．
如图是由5个相同的小正方体组成的几何体，其主视图是（ ）
如图是由5个相同的小正方体组成的几何体，其主视图是（ ）| A． |  | B． |  | C． |  | D． |  |
如图，在平面直角坐标系中，直线y=-$\frac{1}{2}$x+2分别交x轴、y轴于A、B两点，点P（1，m）在△AOB的形内（不包含边界），则m的值可能是1．（填一个即可）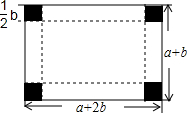
红枣丰收了，为了运输方便，小华的爸爸打算把一个长为（a+2b）cm、宽为（a+b）cm的长方形纸板制成一个有底无盖的盒子，在长方形纸板的四个角各截去一个边长为$\frac{1}{2}$bcm的小正方形，然后沿折线折起即可，如图所示，现将盒子的外表面贴上彩色花板．
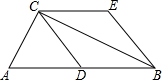如图，在Rt△ABC中，∠ACB=90°，CD是AB边上的中线，过点B作BE∥CD，过点C作CE∥AB，BE，CE相交于点E．