题目内容
17．
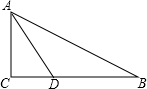如图，在△ABC中，∠C=90°，∠B=30°，BC=6cm，AD是∠CAB的平分线，求DC的长．
分析 由角平分线的定义以及三角形内角和定理可求出∠CAD=∠BAD=∠B=30°，再根据直角三角形30°所对的直角边等于斜边的一半可得AD=2CD，根据等角对等边可得BD=AD，然后利用BC=CD+BD=3CD可求得DC=2cm．
解答 解：∵∠C=90°，∠B=30°，
∴∠CAB=60°．
∵AD是∠CAB的平分线，
∴∠CAD=∠BAD=∠B=30°．
∴AD=2CD，AD=BD．
∴BC=3CD．
∴CD=$\frac{1}{3}BC$=$\frac{1}{3}×6=2$．
∴DC的长为2cm．
点评 本题考查了角平分线上的点到角的两边距离相等的性质，直角三角形30°所对的直角边等于斜边的一半的性质，等角对等边的性质，熟记各性质是解题的关键．
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
已知：如图，$\frac{AD}{AC}=\frac{DE}{AB}=\frac{AE}{BC}$，求证：AB=AE．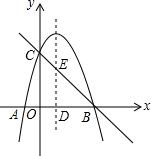
如图，抛物线y=-x2+bx+c交x轴于点B（3，0），交y轴交于点C（0，3），抛物线的对称轴交x轴于点D．
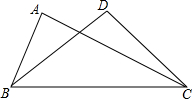如图，在△ABC和△DCB中，AB=DC，下列四个条件：①AC=DB；②∠A=∠B； ③∠ABC=∠DCB；④∠ACB=∠DBC中，添加其中的一个条件不能使△ABC≌△DCB的有（ ）
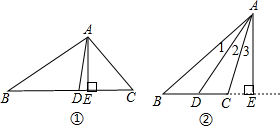求证：三角形一个角的平分线与这个角的对边上的高所形成的夹角等于另两个角之差的一半．
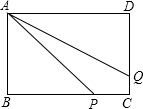如图，在矩形ABCD中，已知AB=$\sqrt{8}$，BC=$\sqrt{18}$，点P在BC上，点Q在CD上，且CP=2CQ，四边形APCQ的面积是7，求BP的长．
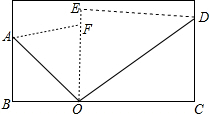将一张矩形纸片按如图方式折叠，设O点是矩形边上一点，将矩形的一角沿OA翻折使OB与OF重合，再将其邻角沿0D翻折，使OC与OE重合，且O、E、F在同一直线上．求OA与∠BOF、OD与∠EOC的关系．
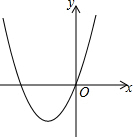已知抛物线的顶点为（-2，-3），且经过原点，
表示a-b+c，图形
表示-x+y-z，则
+
的值为-3．