题目内容
4.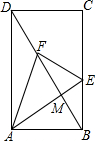 如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )
如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{13}\sqrt{13}$ | D. | $\frac{2}{13}\sqrt{13}$ |
分析 如图,根据垂线段最短可知,当等E与等B重合时,AF⊥BD时,AE+AF最短.只要证明∠1=∠2,根据cos∠EAF=cos∠2=$\frac{AD}{BD}$计算即可.
解答 解:如图,根据垂线段最短可知,当等E与等B重合时,AF⊥BD时,AE+AF最短.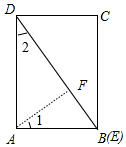
∵∠1+∠DAF=90°,∠2+∠DAF=90°,
∴∠1=∠2,
在Rt△ADB中,BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=$\sqrt{{6}^{2}+{4}^{2}}$=2$\sqrt{13}$,
∴cos∠EAF=cos∠2=$\frac{AD}{BD}$=$\frac{6}{2\sqrt{13}}$=$\frac{3\sqrt{13}}{13}$,
故选C.
点评 本题考查轴对称-最短问题、矩形的性质、勾股定理、锐角三角函数等知识,解题的关键是灵活运用垂线段最短解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
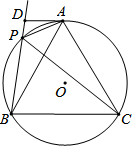 如图,⊙O是等边三角形ABC的外接圆,P是⊙O上一点,D是BP延长线上的一个点,且∠DAP=∠ABP,若AD=4,PD=2,则线段AB的长是2+2$\sqrt{13}$.
如图,⊙O是等边三角形ABC的外接圆,P是⊙O上一点,D是BP延长线上的一个点,且∠DAP=∠ABP,若AD=4,PD=2,则线段AB的长是2+2$\sqrt{13}$. 如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把球向远离灯的位置移动时,圆形阴影面积的大小的变化情况是变小.
如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把球向远离灯的位置移动时,圆形阴影面积的大小的变化情况是变小.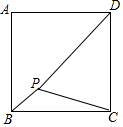 如图,P为正方形ABCD内一点,PB=1,PC=2,∠BPC=135°,求PD的长.
如图,P为正方形ABCD内一点,PB=1,PC=2,∠BPC=135°,求PD的长.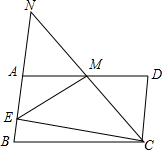 如图,在?ABCD中,BC=2AB,点M是AD的中点,CM的延长线与BA的延长线相交于点N,CE⊥AB于E,连接EM,如果∠AEM=50°,求∠B的度数.
如图,在?ABCD中,BC=2AB,点M是AD的中点,CM的延长线与BA的延长线相交于点N,CE⊥AB于E,连接EM,如果∠AEM=50°,求∠B的度数.