题目内容
14.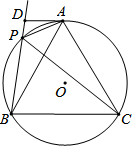 如图,⊙O是等边三角形ABC的外接圆,P是⊙O上一点,D是BP延长线上的一个点,且∠DAP=∠ABP,若AD=4,PD=2,则线段AB的长是2+2$\sqrt{13}$.
如图,⊙O是等边三角形ABC的外接圆,P是⊙O上一点,D是BP延长线上的一个点,且∠DAP=∠ABP,若AD=4,PD=2,则线段AB的长是2+2$\sqrt{13}$.
分析 根据圆内接四边形的性质得到∠APD=∠ACB=60°,过D作DH⊥AP于H,解直角三角形得到PH=1,DH=$\sqrt{3}$,AH=$\sqrt{A{D}^{2}-D{H}^{2}}$=$\sqrt{13}$,AP=1+$\sqrt{13}$,根据相似三角形的性质列方程即可得到结论.
解答  解:∵△ABC是等边三角形,
解:∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠APD=∠ACB=60°,
过D作DH⊥AP于H,
∴∠AHD=∠DHP=90°,
∵PD=2,
∴PH=1,DH=$\sqrt{3}$,
∴AH=$\sqrt{A{D}^{2}-D{H}^{2}}$=$\sqrt{13}$,
∴AP=1+$\sqrt{13}$,
∵∠ADP=∠BPA,∠DAP=∠ABP,
∴△ADP∽△ADB,
∴$\frac{AP}{AB}=\frac{PD}{AD}$,即$\frac{1+\sqrt{13}}{AB}$=$\frac{2}{4}$,
∴AB=2+2$\sqrt{13}$,
故答案为:2+2$\sqrt{13}$.
点评 本题考查了相似三角形的判定与性质、圆周角定理的应用,能够熟练运用相似三角形的判定与性质是解题关键.

练习册系列答案
相关题目
4.下列命题中,真命题是( )
| A. | 六边形的内角和为540度 | B. | 多边形的外角和与边数有关 | ||
| C. | 矩形的对角线互相垂直 | D. | 三角形两边的和大于第三边 |
4.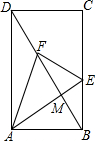 如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )
如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )
 如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )
如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{13}\sqrt{13}$ | D. | $\frac{2}{13}\sqrt{13}$ |
 如图,D、E分别在BC、AC上,AD、BE交于点F,且CD=2BD,CE=3AE,则BF:EF的值为2:1.
如图,D、E分别在BC、AC上,AD、BE交于点F,且CD=2BD,CE=3AE,则BF:EF的值为2:1.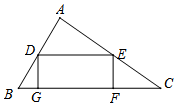 在△ABC中,BC=6,S△ABC=6,矩形DEFG内接于△ABC,其中点G、F在BC上,点D、E分别在AB、AC上,若DE:EF=k,求:四边形DEFG的面积.
在△ABC中,BC=6,S△ABC=6,矩形DEFG内接于△ABC,其中点G、F在BC上,点D、E分别在AB、AC上,若DE:EF=k,求:四边形DEFG的面积.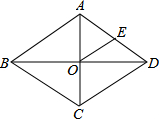 如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于3.5.
如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于3.5.
 如图所示,AB与CD相交于点O,OE平分∠AOD,若∠BOD=40°,求∠AOC,∠AOE的度数.
如图所示,AB与CD相交于点O,OE平分∠AOD,若∠BOD=40°,求∠AOC,∠AOE的度数.