题目内容
9．已知：正比例函数y=kx（k≠0）过A（-2，3），求：（1）比例系数k的值；
（2）在x轴上找一点P，使S△PAO=6，并求点P的坐标．
分析 （1）因为正比例函数y=kx的图象经过点（1，-3），所以-3=k，解之即可解决问题．
（2）设P（x，0），根据题意得出S△PAO=$\frac{1}{2}$×|x|•3=6，解方程即可．
解答 解：（1）∵正比例函数y=kx的图象经过A点（-2，3），
∴-2k=3，
∴k=-$\frac{3}{2}$
∴该正比例函数的解析式为：y=-$\frac{3}{2}$x．
（2）设P（x，0），
∴OP=|x|，
∵S△PAO=6，
∴$\frac{1}{2}$×|x|•3=6，
∴x1=4，x2=-4，
∴P（4，0）或P（-4，0）．
点评 此题主要考查了待定系数法求正比例函数解析式，以及一次函数图象上点的坐标特征，三角形面积等，求得解析式上解题的关键．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
4．
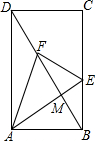如图，在矩形ABCD中，AB=4，BC=6，点E，F分别为线段BC，DB上的动点，DB与AE相交于点M．当AE+AF取最小值时，cos∠EAF的值是（ ）
如图，在矩形ABCD中，AB=4，BC=6，点E，F分别为线段BC，DB上的动点，DB与AE相交于点M．当AE+AF取最小值时，cos∠EAF的值是（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{2}$ | C． | $\frac{3}{13}\sqrt{13}$ | D． | $\frac{2}{13}\sqrt{13}$ |
在一条笔直的公路的同侧依次排列着A，C，B三个村庄，某天甲、乙两车分别从A，B两地出发，沿这条公路匀速行驶至C地停止，从甲车出发至甲车到达C地的过程，甲、乙两车各自与C地的距离y（km）与甲车行驶时间t（h）之间的函数关系如图所示．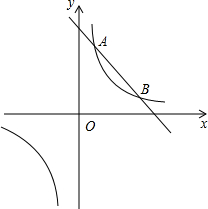
如图，反比例函数y1=$\frac{k}{x}$，（k＞0）与一次函数y2=-x+5交于A（2，n）、B两点（A点在B点左边）