题目内容
19.已知x=3y,求$\frac{4xy}{{x}^{2}-{y}^{2}}$-$\frac{x+y}{x-y}$的值.分析 原式通分并利用同分母分式的减法法则化简,将已知等式代入计算求出值.
解答 解:原式=$\frac{4xy}{(x+y)(x-y)}$-$\frac{(x+y)^{2}}{(x+y)(x-y)}$=-$\frac{(x-y)^{2}}{(x+y)(x-y)}$=$\frac{x-y}{x+y}$,
当x=3y时,原式=$\frac{3y-y}{3y+y}$=$\frac{1}{2}$.
点评 此题考查了分式的化简求值,熟练掌握通分及约分的性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.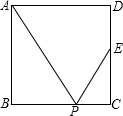 如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP:BC=2:3,其中能推出△ABP∽△ECP的有( )
如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP:BC=2:3,其中能推出△ABP∽△ECP的有( )
 如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP:BC=2:3,其中能推出△ABP∽△ECP的有( )
如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP:BC=2:3,其中能推出△ABP∽△ECP的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.下列图形中一定相似的是( )
| A. | 各有一个锐角相等的两个等腰三角形 | |
| B. | 各有一个角相等的两个菱形 | |
| C. | 四个角对应相等的两个梯形 | |
| D. | 各边对应成比例的两个四边形 |
4.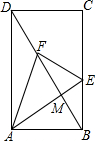 如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )
如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )
 如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )
如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{13}\sqrt{13}$ | D. | $\frac{2}{13}\sqrt{13}$ |
9. 如图,直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )
如图,直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )
 如图,直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )
如图,直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )| A. | (0,42015) | B. | (0,42014) | C. | (0,32015) | D. | (0,32014) |
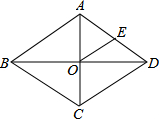 如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于3.5.
如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于3.5. 如图,在?ABCD中,对角线AC,BD相交于点O,△AOB的周长是10cm,AB=3cm,AD=5cm,试求△AOD的周长.
如图,在?ABCD中,对角线AC,BD相交于点O,△AOB的周长是10cm,AB=3cm,AD=5cm,试求△AOD的周长. 如图所示,矩形ABCD的对角线AC,BD的交点O,点E、F、G、H分别是AO、BO、OC、OD的中点.
如图所示,矩形ABCD的对角线AC,BD的交点O,点E、F、G、H分别是AO、BO、OC、OD的中点.