题目内容
16.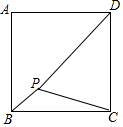 如图,P为正方形ABCD内一点,PB=1,PC=2,∠BPC=135°,求PD的长.
如图,P为正方形ABCD内一点,PB=1,PC=2,∠BPC=135°,求PD的长.
分析 将△PBC沿C点顺时针旋转90°,此时B与D点重合,P点旋转到P'点,连接PP',易证△PCP'是等腰直角三角形,所以利用勾股定理可求出P'P的长,在证明△PP'D是直角三角形.利用勾股定理求出PD的长即可.
解答 解:
将△PBC沿C点顺时针旋转90°,此时B与D点重合,P点旋转到P'点,连接PP'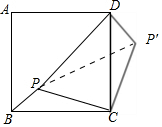
∴PC=P'C=2,BP=DP′=1,
∴△PCP'是等腰直角三角形,
∴∠PP'C=45°,
∴PP'=$\sqrt{2}$PC=2$\sqrt{2}$,
又∵∠DP'C=∠BPC=135°,
∴∠PP'D=135°-45°=90°,
∴在直角△PP'D中,PD=$\sqrt{DP{′}^{2}+PP{′}^{2}}$=3.
点评 本题考查了正方形的性质、旋转的性质、等腰直角三角形的判断和性质以及勾股定理的运用,解答此题的关键是利用旋转构建直角三角形,由勾股定理求解.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
7.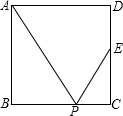 如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP:BC=2:3,其中能推出△ABP∽△ECP的有( )
如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP:BC=2:3,其中能推出△ABP∽△ECP的有( )
 如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP:BC=2:3,其中能推出△ABP∽△ECP的有( )
如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP:BC=2:3,其中能推出△ABP∽△ECP的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.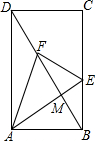 如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )
如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )
 如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )
如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{13}\sqrt{13}$ | D. | $\frac{2}{13}\sqrt{13}$ |
5.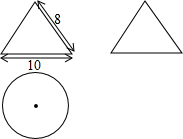 如图,按照三视图确定该几何体的侧面积是(图中尺寸单位:cm)( )
如图,按照三视图确定该几何体的侧面积是(图中尺寸单位:cm)( )
 如图,按照三视图确定该几何体的侧面积是(图中尺寸单位:cm)( )
如图,按照三视图确定该几何体的侧面积是(图中尺寸单位:cm)( )| A. | 40πcm2 | B. | 65πcm2 | C. | 80πcm2 | D. | 105πcm2 |
6.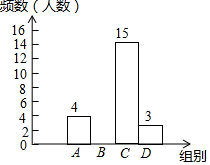 为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
(1)图中a=4,这次比赛成绩的众数落在C组;
(2)请补全频数分布直方图;
(3)学校决定选派本次比赛成绩最好的3人参加全市中学生朗诵比赛,并为参赛选手准备了2件白色、1件蓝色上衣和黑色、蓝色、白色的裤子各1条,小军先选,他从中随机选取一件上衣和一条裤子搭配成一套衣服,请用画树状图法或列表法求出上衣和裤子搭配成不同颜色的概率.
 为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题. | 组别 | 成绩x(分) | 频数(人数) |
| A | 8.0≤x<8.5 | a |
| B | 8.5≤x<9.0 | 8 |
| C | 9.0≤x<9.5 | 15 |
| D | 9.5≤x<10 | 3 |
(2)请补全频数分布直方图;
(3)学校决定选派本次比赛成绩最好的3人参加全市中学生朗诵比赛,并为参赛选手准备了2件白色、1件蓝色上衣和黑色、蓝色、白色的裤子各1条,小军先选,他从中随机选取一件上衣和一条裤子搭配成一套衣服,请用画树状图法或列表法求出上衣和裤子搭配成不同颜色的概率.
 如图所示,AB与CD相交于点O,OE平分∠AOD,若∠BOD=40°,求∠AOC,∠AOE的度数.
如图所示,AB与CD相交于点O,OE平分∠AOD,若∠BOD=40°,求∠AOC,∠AOE的度数.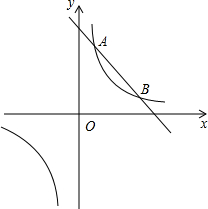 如图,反比例函数y1=$\frac{k}{x}$,(k>0)与一次函数y2=-x+5交于A(2,n)、B两点(A点在B点左边)
如图,反比例函数y1=$\frac{k}{x}$,(k>0)与一次函数y2=-x+5交于A(2,n)、B两点(A点在B点左边) 如图所示,矩形ABCD的对角线AC,BD的交点O,点E、F、G、H分别是AO、BO、OC、OD的中点.
如图所示,矩形ABCD的对角线AC,BD的交点O,点E、F、G、H分别是AO、BO、OC、OD的中点.