题目内容
14.先化简,再求值:$\frac{a^2}{{{a^2}+2a}}$-$\frac{{{a^2}-2a+1}}{a+2}$÷$\frac{{{a^2}-1}}{a+1}$,其中a=cos30°-2tan45°.分析 先算除法,再算减法,最后求出a的值代入进行计算即可.
解答 解:原式=$\frac{a}{a+2}$-$\frac{(a-1)^{2}}{a+2}$•$\frac{1}{a-1}$
=$\frac{a}{a+2}$-$\frac{a-1}{a+2}$
=$\frac{1}{a+2}$,
当a=cos30°-2tan45°=$\frac{\sqrt{3}}{2}$-2时,原式=$\frac{1}{\frac{\sqrt{3}}{2}}$=$\frac{2\sqrt{3}}{3}$.
点评 本题考查的是分式的化简求值及特殊角的三角函数值,在解答此类题目时要把分式化为最简形式,再代入求值.

练习册系列答案
相关题目
4.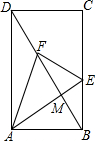 如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )
如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )
 如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )
如图,在矩形ABCD中,AB=4,BC=6,点E,F分别为线段BC,DB上的动点,DB与AE相交于点M.当AE+AF取最小值时,cos∠EAF的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{13}\sqrt{13}$ | D. | $\frac{2}{13}\sqrt{13}$ |
5.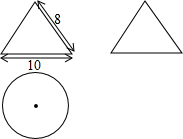 如图,按照三视图确定该几何体的侧面积是(图中尺寸单位:cm)( )
如图,按照三视图确定该几何体的侧面积是(图中尺寸单位:cm)( )
 如图,按照三视图确定该几何体的侧面积是(图中尺寸单位:cm)( )
如图,按照三视图确定该几何体的侧面积是(图中尺寸单位:cm)( )| A. | 40πcm2 | B. | 65πcm2 | C. | 80πcm2 | D. | 105πcm2 |
9. 如图,直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )
如图,直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )
 如图,直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )
如图,直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )| A. | (0,42015) | B. | (0,42014) | C. | (0,32015) | D. | (0,32014) |
6.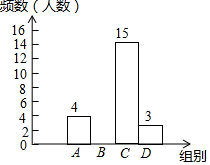 为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
(1)图中a=4,这次比赛成绩的众数落在C组;
(2)请补全频数分布直方图;
(3)学校决定选派本次比赛成绩最好的3人参加全市中学生朗诵比赛,并为参赛选手准备了2件白色、1件蓝色上衣和黑色、蓝色、白色的裤子各1条,小军先选,他从中随机选取一件上衣和一条裤子搭配成一套衣服,请用画树状图法或列表法求出上衣和裤子搭配成不同颜色的概率.
 为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题. | 组别 | 成绩x(分) | 频数(人数) |
| A | 8.0≤x<8.5 | a |
| B | 8.5≤x<9.0 | 8 |
| C | 9.0≤x<9.5 | 15 |
| D | 9.5≤x<10 | 3 |
(2)请补全频数分布直方图;
(3)学校决定选派本次比赛成绩最好的3人参加全市中学生朗诵比赛,并为参赛选手准备了2件白色、1件蓝色上衣和黑色、蓝色、白色的裤子各1条,小军先选,他从中随机选取一件上衣和一条裤子搭配成一套衣服,请用画树状图法或列表法求出上衣和裤子搭配成不同颜色的概率.
3.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. | 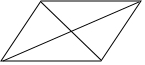 | C. | 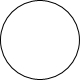 | D. |  |
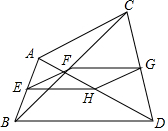 如图,在四边形ABDC中,E,F,G,H分别为AB,BC,CD,DA的中点,并且E,F,G,H四点不共线.
如图,在四边形ABDC中,E,F,G,H分别为AB,BC,CD,DA的中点,并且E,F,G,H四点不共线.