题目内容
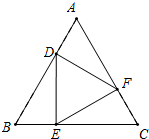 如图,在边长为3的等边△ABC中,D、E、F分别是AB、BC、AC上的点,AD=BE=CF=1.
如图,在边长为3的等边△ABC中,D、E、F分别是AB、BC、AC上的点,AD=BE=CF=1.(1)求证:△DEF是等边三角形;
(2)猜想DE与BC的位置关系,并加以验证.
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)根据等边△ABC中AD=BE=CF,证得△ADF≌△BED≌△CFE即可得出:△DEF是等边三角形;
(2)假设△BDE是直角三角形,令∠BED是直角,则BE2+DE2=BD2,根据勾股定理列方程,解答出即可.
(2)假设△BDE是直角三角形,令∠BED是直角,则BE2+DE2=BD2,根据勾股定理列方程,解答出即可.
解答:(1)证明:∵△ABC为等边三角形,且AD=BE=CF
∴AF=BD=CE,
在△ADF和△BED和△CFE中,
,
∴△ADF≌△BED≌△CFE(SAS),
∴DF=ED=EF,
∴△DEF是一个等边三角形.
(2)如果△BDE是直角三角形,令∠BED是直角,根据勾股定理的逆定理得:BE2+DE2=BD2,设BD=x,
则(
x)2+(3-x)2=x2,
解得,x1=6(舍去),x2=2;
所以BD=BC-AD=2时,△BDE是直角三角形.
即DE⊥BC.
∴AF=BD=CE,
在△ADF和△BED和△CFE中,
|
∴△ADF≌△BED≌△CFE(SAS),
∴DF=ED=EF,
∴△DEF是一个等边三角形.
(2)如果△BDE是直角三角形,令∠BED是直角,根据勾股定理的逆定理得:BE2+DE2=BD2,设BD=x,
则(
| ||
| 2 |
解得,x1=6(舍去),x2=2;
所以BD=BC-AD=2时,△BDE是直角三角形.
即DE⊥BC.
点评:此题主要考查了等边三角形的判定与性质和全等三角形判定,以及勾股定理的运用,根据已知得出△ADF≌△BED≌△CFE是解题关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、对角线相等且互相垂直的四边形是菱形 |
| B、对角线相等的四边形是矩形 |
| C、若a2=b2,则a=b |
| D、相似三角形对应高的比等于周长的比 |
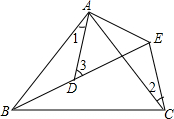 如图,AB=AC,AD=AE,∠BAC=∠DAE,B、D、E三点在同一条直线上且∠1=25°,∠2=30°,则∠3=
如图,AB=AC,AD=AE,∠BAC=∠DAE,B、D、E三点在同一条直线上且∠1=25°,∠2=30°,则∠3= 如图,已知a∥b,直线c与a,b相交,若∠1=60°,则∠2=
如图,已知a∥b,直线c与a,b相交,若∠1=60°,则∠2=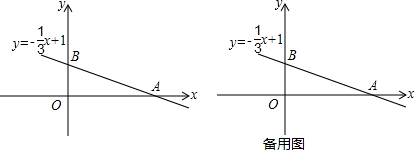
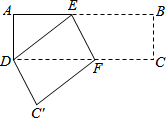 在长方形纸片ABCD中,AD=3cm,AB=9cm,按如图方式折叠,使点B与点D重合,折痕为EF,则DE=
在长方形纸片ABCD中,AD=3cm,AB=9cm,按如图方式折叠,使点B与点D重合,折痕为EF,则DE=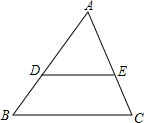 如图,已知DE∥BC,AD=5,DB=3,则S△ADE:S四边形DBCE=
如图,已知DE∥BC,AD=5,DB=3,则S△ADE:S四边形DBCE=
