题目内容
 如图,已知圆的半径为r,求外接正六边形的边长.
如图,已知圆的半径为r,求外接正六边形的边长.考点:正多边形和圆
专题:
分析:首先连接OA,OB,OC,由外接正六边形的性质,可证得△OAB是等边三角形,继而求得答案.
解答: 解:如图,连接OA,OB,OC,则∠AOB=
解:如图,连接OA,OB,OC,则∠AOB=
=60°,
∵⊙O是内切圆,
∴OC⊥AB,
∵OA=OB,
∴△AOB是等边三角形,
∴OA=AB=OB,∠OAB=60°,
∵OC=r,
∴OA=
=
r,
∴AB=
r.
即外接正六边形的边长为:
r.
 解:如图,连接OA,OB,OC,则∠AOB=
解:如图,连接OA,OB,OC,则∠AOB=| 360° |
| 6 |
∵⊙O是内切圆,
∴OC⊥AB,
∵OA=OB,
∴△AOB是等边三角形,
∴OA=AB=OB,∠OAB=60°,
∵OC=r,
∴OA=
| OC |
| sin60° |
2
| ||
| 3 |
∴AB=
2
| ||
| 3 |
即外接正六边形的边长为:
2
| ||
| 3 |
点评:此题考查了圆的外接正六边形的性质以及等边三角形的判定与性质.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
已知(a+b)2=11,(a-b)2=7,则a2+b2等于( )
| A、4 | B、18 | C、9 | D、8 |
关于x的方程x2-(m-1)x+m-6=0,对其根的情况叙述,正确的是( )
| A、有两个相等的实数根 |
| B、有两个不相等的实数根 |
| C、没有实数根 |
| D、不能确定 |
在直线AB上有一点C,已知CB=2cm,AB=4cm,则AC等于( )
| A、6cm | B、2cm |
| C、6cm或2cm | D、无法确定 |
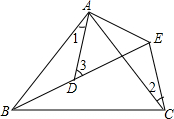 如图,AB=AC,AD=AE,∠BAC=∠DAE,B、D、E三点在同一条直线上且∠1=25°,∠2=30°,则∠3=
如图,AB=AC,AD=AE,∠BAC=∠DAE,B、D、E三点在同一条直线上且∠1=25°,∠2=30°,则∠3=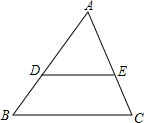 如图,已知DE∥BC,AD=5,DB=3,则S△ADE:S四边形DBCE=
如图,已知DE∥BC,AD=5,DB=3,则S△ADE:S四边形DBCE=

 如图,已知正n边形边长为a,边心距为r,求正n边形的半径R、周长P和面积S.
如图,已知正n边形边长为a,边心距为r,求正n边形的半径R、周长P和面积S.