题目内容
 如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,
如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,①猜想DE与AB的关系?并加以证明;
②若P是AB延长线一点,Q为BC一点,其他条件不变,结论成立吗?画图并证明.
(友情引导:若不知道,你可以动手去量发现结论.若不会,P是动点,你可以把P运动到特殊的地方,发现现在可利用什么性质?接下来证明.发现缺少什么?就补什么?若还不会,你能发现有线段相等吗?尝试证明,你会有惊喜.)
考点:全等三角形的判定与性质,等边三角形的性质
专题:动点型
分析:(1)过P做BC的平行线至AC于F,可证△PFD≌△QCD,即可得FD=CD,即可求得AB=2DE;
(2)和(1)求解方法相同,注意根据题意画出图形.
(2)和(1)求解方法相同,注意根据题意画出图形.
解答:解:(1)过P做BC的平行线至AC于F,
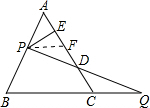
∵PF∥BC,∴△APF为等边三角形,
∵PE⊥AF,∴AE=EF
∵AP=PF,QP=CQ,
∴PF=CQ,
在△PFD和△QCD中,
,
∴△PFD≌△QCD(AAS),
∴FD=CD,
∴AC=DE+AE+CD=DE+EF+FD=2DE.
∴AB=2DE.
(2)过P做BC的平行线至AC于F,
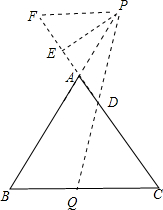
∵PF∥BC,∴△APF为等边三角形,
∵PE⊥AF,∴AE=EF
∵AP=PF,QP=CQ,
∴PF=CQ,
在△PFD和△QCD中,
,
∴△PFD≌△QCD(AAS),
∴FD=CD,
∴AC=CD+AD=DF+AD=DE+EF+AD=DE+AE+AD=2DE.
∴AB=2DE.

∵PF∥BC,∴△APF为等边三角形,
∵PE⊥AF,∴AE=EF
∵AP=PF,QP=CQ,
∴PF=CQ,
在△PFD和△QCD中,
|
∴△PFD≌△QCD(AAS),
∴FD=CD,
∴AC=DE+AE+CD=DE+EF+FD=2DE.
∴AB=2DE.
(2)过P做BC的平行线至AC于F,

∵PF∥BC,∴△APF为等边三角形,
∵PE⊥AF,∴AE=EF
∵AP=PF,QP=CQ,
∴PF=CQ,
在△PFD和△QCD中,
|
∴△PFD≌△QCD(AAS),
∴FD=CD,
∴AC=CD+AD=DF+AD=DE+EF+AD=DE+AE+AD=2DE.
∴AB=2DE.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了等边三角形的性质.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
关于x的方程x2-(m-1)x+m-6=0,对其根的情况叙述,正确的是( )
| A、有两个相等的实数根 |
| B、有两个不相等的实数根 |
| C、没有实数根 |
| D、不能确定 |
 如图,已知a∥b,直线c与a,b相交,若∠1=60°,则∠2=
如图,已知a∥b,直线c与a,b相交,若∠1=60°,则∠2=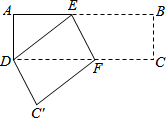 在长方形纸片ABCD中,AD=3cm,AB=9cm,按如图方式折叠,使点B与点D重合,折痕为EF,则DE=
在长方形纸片ABCD中,AD=3cm,AB=9cm,按如图方式折叠,使点B与点D重合,折痕为EF,则DE=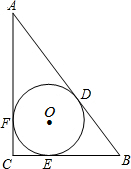 如图,⊙O为△ABC的内切圆,D、E、F分别为切点,已知∠C=90°,⊙O的半径长为3cm,AC=10cm,则AD长度为
如图,⊙O为△ABC的内切圆,D、E、F分别为切点,已知∠C=90°,⊙O的半径长为3cm,AC=10cm,则AD长度为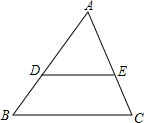 如图,已知DE∥BC,AD=5,DB=3,则S△ADE:S四边形DBCE=
如图,已知DE∥BC,AD=5,DB=3,则S△ADE:S四边形DBCE=