题目内容
7.根据如图给出的数轴,解答下面的问题:(1)请你根据图中A、B两点的位置,分别写出它们所表示的有理数A:1;B:-2.5;

(2)观察数轴,与点A的距离为4的点表示的数是:-3或5;
(3)若将数轴折叠,使得A点与-3表示的点重合,则B点与数0.5表示的点重合;
(4)若数轴上M、N两点之间的距离为2016(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M:-1009 N:1007
(5)若数轴上M、N两点之间的距离为a(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M:-1-$\frac{1}{2}$a N:-1+$\frac{1}{2}$a.
分析 (1)观察数轴可得;
(2)分点A左边4个单位和右边4个单位两种情况;
(3)根据点A与-3表示的点重合可得对称中心,继而可得点B关于-1对称的点;
(4)根据题意得出M、N两点到对称中心的距离,继而由对称中心分别向左和向右得出点M、N所表示的数;
(5)与(4)同理可得.
解答 解:(1)由数轴可知点A表示数1,点B表示数-2.5,
故答案为:1,-2.5;
(2)与点A的距离为4的点表示的数是-3或5,
故答案为:-3或5;
(3)∵将数轴折叠,A点与-3表示的点重合,
∴对称中心为-1,
∴点B与数0.5重合,
故答案为:0.5;
(4)∵数轴上M、N两点之间的距离为2016,
∴M、N两点间的距离为1008,
若沿数-1表示的点重合,
则点M表示数-1009,点N表示数1007,
故答案为:-1009,1007;
(5)∵数轴上M、N两点之间的距离为a,
∴M、N两点间的距离为$\frac{1}{2}$a,
若沿数-1表示的点重合,
则点M表示数-1-$\frac{1}{2}$a,点N表示数-1+$\frac{1}{2}$a,
故答案为:-1-$\frac{1}{2}$a,-1+$\frac{1}{2}$a.
点评 本题考查了数轴,解答此题的关键是利用了数轴上两点间的距离,中心对称,注意(2)要分情况讨论.

练习册系列答案
相关题目
17.下列运算正确的是( )
| A. | 2ab+3ab=5a2b2 | B. | a2•a3=a6 | C. | a-2=$\frac{1}{{a}^{2}}$(a≠0) | D. | $\sqrt{x+y}=\sqrt{x}+\sqrt{y}$ |
15.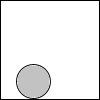 如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )
如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )
 如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )
如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )| A. | a2-π | B. | 4-π | C. | π | D. | (4-π)a2 |
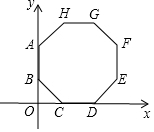 如图,正八边形的边长为2,点C的坐标是($\sqrt{2}$,0).
如图,正八边形的边长为2,点C的坐标是($\sqrt{2}$,0).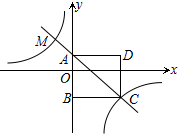 如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,-2),反比例函数y=$\frac{k}{x}$的图象经过点C,一次函数y=ax+b的图象经过A、C两点.
如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,-2),反比例函数y=$\frac{k}{x}$的图象经过点C,一次函数y=ax+b的图象经过A、C两点.