题目内容
19.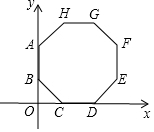 如图,正八边形的边长为2,点C的坐标是($\sqrt{2}$,0).
如图,正八边形的边长为2,点C的坐标是($\sqrt{2}$,0).(1)写出其余各点的坐标;
(2)如果在(1)中作出正八边形关于x轴对称的图形,则可以得到一个“8”字形,试写出这个“8”字形另外六个顶点的坐标;
(3)试换一个点为原点,建立另一个坐标系,并写出各个顶点的坐标.
分析 (1)由正八边形的性质即可得出各个顶点的坐标;
(2)作出图形,容易得出各个顶点坐标;
(3)以C为原点,建立直角坐标系,容易得出各个顶点坐标.
解答 解:(1)∵正八边形的边长为2,点C的坐标是($\sqrt{2}$,0).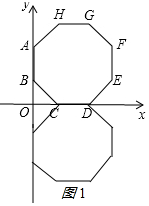
∴OB=OC=$\sqrt{2}$,OA=OD=2+$\sqrt{2}$,
∴A(0,2+$\sqrt{2}$),B(0,$\sqrt{2}$),D(2+$\sqrt{2}$,0),E(2+2$\sqrt{2}$,$\sqrt{2}$),
F(2+2$\sqrt{2}$,2+$\sqrt{2}$),G(2+$\sqrt{2}$,2+2$\sqrt{2}$),H($\sqrt{2}$,2+2$\sqrt{2}$);
(2)正八边形关于x轴对称的图形,
如图1所示:
另外六个顶点的坐标分别为(0,-2-$\sqrt{2}$),(0,-$\sqrt{2}$),(2+2$\sqrt{2}$,-$\sqrt{2}$),(2+2$\sqrt{2}$,-2-$\sqrt{2}$),(2+$\sqrt{2}$,-2-2$\sqrt{2}$),($\sqrt{2}$,-2-2$\sqrt{2}$);
(3)以C为原点,建立直角坐标系,
如图2所示:
各个顶点的坐标分别为A(-$\sqrt{2}$,2+$\sqrt{2}$),B(-$\sqrt{2}$,$\sqrt{2}$),C(0,0),D(2+$\sqrt{2}$,0),
E(2+$\sqrt{2}$,$\sqrt{2}$),F(2+$\sqrt{2}$,2+$\sqrt{2}$),G(2,2+2$\sqrt{2}$),H(0,2+2$\sqrt{2}$).
点评 本题考查的是正多边形的性质、轴对称图形以及关于x轴得出的点的坐标;熟练掌握正八边形的性质是解决问题的关键.

 全能练考卷系列答案
全能练考卷系列答案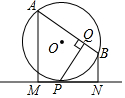 如图,MN切⊙O的弦于P,AB是⊙O的弦,AM⊥MN于M,BN⊥MN于N,PQ⊥AB于Q,求证:PQ2=AM•BN.
如图,MN切⊙O的弦于P,AB是⊙O的弦,AM⊥MN于M,BN⊥MN于N,PQ⊥AB于Q,求证:PQ2=AM•BN.
 如图,△ABC中,AB=AC,∠C=30°,DA⊥BA于A,BC=6cm,求AD的长.
如图,△ABC中,AB=AC,∠C=30°,DA⊥BA于A,BC=6cm,求AD的长. 如图,在△ABC中,AB=AC,AG是BC边上的高,D是AB上一点,过D作DE⊥BC、ED的延长线交CA的延长线于点F,求证:AD=AF.
如图,在△ABC中,AB=AC,AG是BC边上的高,D是AB上一点,过D作DE⊥BC、ED的延长线交CA的延长线于点F,求证:AD=AF.