题目内容
9.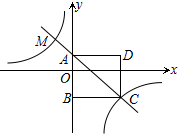 如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,-2),反比例函数y=$\frac{k}{x}$的图象经过点C,一次函数y=ax+b的图象经过A、C两点.
如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,-2),反比例函数y=$\frac{k}{x}$的图象经过点C,一次函数y=ax+b的图象经过A、C两点.(1)AB=3,点C的坐标为(3,-2),反比例函数的解析式为y=-$\frac{6}{x}$,一次函数的解析式为y=-x+1.
(2)若点P是y轴正半轴上一点,△AMP的面积恰好等于正方形ABCD的面积,求P点的坐标.
分析 (1)直接根据数轴上两点间的距离公式可得出AB的长,再由正方形的性质得出C点坐标,利用待定系数法求出反比例函数与一次函数的解析式即可;
(2)求出M点的坐标,设P(0,y),再利用三角形的面积公式即可得出结论.
解答 解:(1)∵点A的坐标为(0,1),点B的坐标为(0,-2),
∴AB=|1+2|=3;
∵四边形ABCD为正方形,
∴C(3,-2);
∵反比例函数y=$\frac{k}{x}$的图象经过点C,
∴k=3×(-2)=-6,
∴反比例函数的解析式为y=-$\frac{6}{x}$;
∵点A的坐标为(0,1),C(3,-2)在一次函数y=ax+b的图象上,
∴$\left\{\begin{array}{l}{b=1}\\{3a+b=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=1}\end{array}\right.$,
∴一次函数的解析式为:y=-x+1.
故答案为:3,(3,-2),y=-$\frac{6}{x}$,y=-x+1;
(2)∵由题意得,$\left\{\begin{array}{l}{y=-\frac{6}{x}}\\{y=-x+1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$,
∴M(-2,3)
设P(0,y),
∵S正方形ABCD=9,
∴$\frac{1}{2}$AP×2=9,即$\frac{1}{2}$|y-1|=9,解得y=19或y=17,
∴P(0,19)或(0,17).
点评 本题考查的是反比例函数与一次函数的交点问题,熟知待定系数法求一次函数及反比例函数的解析式是解答此题的关键.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +0.3 | +0.1 | -0.2 | -0.5 | +0.6 |
(2)已知买进股票时需付买入成交额0.15%的手续费,卖出股票时需付卖出成交额0.25%的交易费,如果在本周五收盘时将全部股票一次性地卖出,那么该股民的收益情况如何?

 如图,在△ABC中,AB=AC,AG是BC边上的高,D是AB上一点,过D作DE⊥BC、ED的延长线交CA的延长线于点F,求证:AD=AF.
如图,在△ABC中,AB=AC,AG是BC边上的高,D是AB上一点,过D作DE⊥BC、ED的延长线交CA的延长线于点F,求证:AD=AF. 如图,在△ABC中,AB=AC,D是BC的中点,点E在AD上,找出图中的全等三角形,并证明它们全等.
如图,在△ABC中,AB=AC,D是BC的中点,点E在AD上,找出图中的全等三角形,并证明它们全等.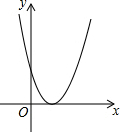 已知二次函数y=ax2+bx+c的图象如图所示,则a>0,b<0,c>0,△=0.(用“<”,“=”或“>”号连接)
已知二次函数y=ax2+bx+c的图象如图所示,则a>0,b<0,c>0,△=0.(用“<”,“=”或“>”号连接) 如图所示的是某个几何体从三种不同方向所看到的图形.
如图所示的是某个几何体从三种不同方向所看到的图形.