题目内容

17．计算：
（1）$\frac{{a}^{2}}{a-1}$-a-1．
（2）$\left\{\begin{array}{l}{2x+3＞x}\\{\frac{1}{2}x≥x-3}\end{array}\right.$．

分析 （1）根据先把异分母转化成同分母，然后进行加减运算；
（2）根据解不等式，可得每个不等式的解集解集，根据不等式解集的公共部分是不等式组的解集，可得答案．

解答 解（1）原式=$\frac{{a}^{2}}{a-1}$-$\frac{（a+1）（a-1）}{a-1}$=$\frac{{a}^{2}-{a}^{2}+1}{a-1}$=$\frac{1}{a-1}$；
（2）由2x+3＞x，解得x＞-3，
由$\frac{1}{2}$x≥x-3，解得x≤6，
不等式组的解集为-3＜x≤6．

点评 本题考查了分式的加减，分式的加减运算中，如果是同分母分式，那么分母不变，把分子直接相加减即可；如果是异分母分式，则必须先通分，把异分母分式化为同分母分式，然后再相加减．

练习册系列答案
相关题目
7．计算：（12a2b-4ab）÷4ab．
8．观察下列数列，找出规律后，写出数列下一项：0，3，-3，9，-15，33，-63，129．
5．已知a＜0，-b＞0，且|b|＜|a|，c是-b的相反数，试比较a，-b，c的大小，并将它们用“＜”连接起来．
12．化简求值：（2x+1）2-（2x+1）（2x-1），其中x=-$\frac{1}{2}$．
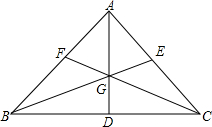2．如图在△ABC中，点D、E、F分别在三边上，E是AC中点．AD、BE、CF交于点G，BD=2DC，S△GCE=4，S△GCD=5，求△ABC的面积？
思路1：由E为AC中点，得S△ACE=4
从而S△ACD=S△GAE+S△GCE+S△GCD=4+4+5=13
∵BD=2DC∴BC=3DC
∴S△ABC=3S△ACD=3×13=39
思路2：∵BD=2DC∴BC=3DC
∴S△GBC=3S△GCD=3×5=15
∴S△BCE=S△GBC+S△GCE=15+4=19
又∵E为AC中点，
∴S△ABC=2S△BCE=2×19=38
问题：上面这道题目用两种不同的思路来求解．但得到的结果却不同．问题出在哪里？如思路有问题．请纠正；若思路没有问题．请探究问题出在哪里？并说明理由．
9．计算：
（1）$\sqrt{15}$÷$\sqrt{\frac{5}{3}}$×$\sqrt{\frac{3}{2}}$                
（2）$\sqrt{12}$+$\sqrt{18}$-$\sqrt{8}$-$\sqrt{32}$
（3）（2$\sqrt{\frac{1}{27}}$-$\frac{2}{3}$$\sqrt{18}$）-（$\sqrt{\frac{4}{3}}$-4$\sqrt{\frac{1}{2}}$）             
（4）（3-2$\sqrt{5}$）2-（$\sqrt{3}$+2）（$\sqrt{3}$-2）
6．（1）如图1，车尾灯内两面镜子AB、BC互相垂直，当光线经过镜子反射时，∠1=∠2，∠3=∠4．说明为什么进入车尾灯的光线与离开车尾灯的光线互相平行；
（2）小明受车尾灯设计启发，进行实验尝试．
①如图2，两面镜子的夹角为α°（0＜α＜90）时，进入光线与离开光线的夹角为β°（0＜β＜90）．试探索α与β的数量关系．
②两面镜子的夹角为α°（90＜α＜180）时，进入光线与离开光线所在直线的夹角为β°（0＜β＜90）．请直接写出α与β的数量关系．2α-β=180°
7．梯形ABCD中，AD∥BC，AB=CD，∠B=60°，AD=10，BC=18，则梯形ABCD的周长是（　　）
A．42B．44C．48D．46

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网