题目内容
9.计算:(1)$\sqrt{15}$÷$\sqrt{\frac{5}{3}}$×$\sqrt{\frac{3}{2}}$
(2)$\sqrt{12}$+$\sqrt{18}$-$\sqrt{8}$-$\sqrt{32}$
(3)(2$\sqrt{\frac{1}{27}}$-$\frac{2}{3}$$\sqrt{18}$)-($\sqrt{\frac{4}{3}}$-4$\sqrt{\frac{1}{2}}$)
(4)(3-2$\sqrt{5}$)2-($\sqrt{3}$+2)($\sqrt{3}$-2)
分析 (1)利用二次根式的乘除法计算即可;
(2)(3)先化简,再进一步合并即可;
(4)利用完全平方公式和平方差公式计算,再进一步合并即可.
解答 解:(1)原式=3×$\sqrt{\frac{3}{2}}$
=$\frac{3}{2}$$\sqrt{6}$;
(2)原式=2$\sqrt{3}$+3$\sqrt{2}$-2$\sqrt{2}$-4$\sqrt{2}$
=2$\sqrt{3}$-3$\sqrt{2}$;
(3)原式=$\frac{2}{9}$$\sqrt{3}$-2$\sqrt{2}$-$\frac{2}{3}$$\sqrt{3}$+2$\sqrt{2}$
=-$\frac{4}{9}$$\sqrt{3}$;
(4)原式=29+12$\sqrt{5}$-3+4
=30+12$\sqrt{5}$.
点评 此题考查二次根式的混合运算,在进行此类运算时,一般先把二次根式化为最简二次根式的形式后再运算.

练习册系列答案
相关题目
20.寒假期间,九(1)班n名同学为了相互表达春节的祝愿,约定每两名同学之间互发一次信息,那么互发信息的总次数m与n的函数关系式可以表示为( )
| A. | m=$\frac{1}{2}$n(n+1) | B. | m=$\frac{1}{2}$n(n-1) | C. | m=$\frac{1}{2}$n2 | D. | m=n(n-1) |
18.三个连续奇数之和为15,则它们之积为( )
| A. | 15 | B. | 21 | C. | 105 | D. | -105 |
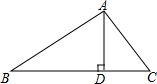 在△ABC中,AD是高,∠C=45°,AC=3$\sqrt{2}$,BD=4,求AB的长.
在△ABC中,AD是高,∠C=45°,AC=3$\sqrt{2}$,BD=4,求AB的长.