题目内容
2.某广场用同一种如图所示的地砖拼图案,第一次拼成形如图1所示的图案,第二次拼成形如图2所示的图案,第三次拼成形如图3所示的图案,第四次拼成形如图4所示的图案…按照这样的规律进行下去,第n次拼成的图案共用地砖2n2+2n块.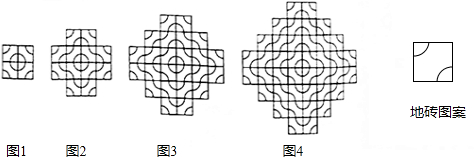
分析 首先求出第一个、第二个、第三个、第四个图案中的地砖的数量,探究规律后即可解决问题.
解答 解:第一次拼成形如图1所示的图案共有4块地砖,4=2×(1×2),
第二拼成形如图2所示的图案共有12块地砖,12=2×(2×3),
第三次拼成形如图3所示的图案共有24块地砖,24=2×(3×4),
第四次拼成形如图4所示的图案共有40块地砖,40=2×(4×5),
…
第n次拼成形如图1所示的图案共有2×n(n+1)=2n2+2n块地砖,
故答案为2n2+2n.
点评 本题考查规律题目、解题的关键是学会从特殊到一般的探究方法,属于中考填空题中的压轴题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13. 如图,BC∥DE,若∠A=35°,∠C=24°,则∠E等于( )
如图,BC∥DE,若∠A=35°,∠C=24°,则∠E等于( )
 如图,BC∥DE,若∠A=35°,∠C=24°,则∠E等于( )
如图,BC∥DE,若∠A=35°,∠C=24°,则∠E等于( )| A. | 24° | B. | 59° | C. | 60° | D. | 69° |
17.若1-$\sqrt{3}$是方程x2-2x+c=0的一个根,则c的值为( )
| A. | -2 | B. | 4$\sqrt{3}$-2 | C. | 3-$\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
7.可燃冰,学名叫“天然气水合物”,是一种高效清洁、储量巨大的新能源.据报道,仅我国可燃冰预测远景资源量就超过了1000亿吨油当量.将1000亿用科学记数法可表示为( )
| A. | 1×103 | B. | 1000×108 | C. | 1×1011 | D. | 1×1014 |
14.下列计算正确的是( )
| A. | (a+2)(a-2)=a2-2 | B. | (a+1)(a-2)=a2+a-2 | C. | (a+b)2=a2+b2 | D. | (a-b)2=a2-2ab+b2 |
17.为了奖励在艺术节活动中表现突出的同学,七(1)班班主任曾两次到多福居给同学们买牛奶和面包,具体数量与金额如表所示:
(1)求牛奶和面包的单价分别是多少元?
(2)该店某天开展优惠促销活动:牛奶每箱6瓶,每买1箱送1瓶;面包全场八折,假设牛奶只能整箱购买.七(1)班共有56名学生.
①若要使每名学生各分得牛奶1瓶和面包1个,共需要多少元钱?
②若要使每名学生至少分得1瓶牛奶和1个面包,共花费560元,求购买的牛奶是多少瓶?面包是多少个?
| 次数 | 牛奶(瓶) | 面包(个) | 总金额(元) |
| 第1次 | 30 | 50 | 430 |
| 第2次 | 20 | 60 | 420 |
(2)该店某天开展优惠促销活动:牛奶每箱6瓶,每买1箱送1瓶;面包全场八折,假设牛奶只能整箱购买.七(1)班共有56名学生.
①若要使每名学生各分得牛奶1瓶和面包1个,共需要多少元钱?
②若要使每名学生至少分得1瓶牛奶和1个面包,共花费560元,求购买的牛奶是多少瓶?面包是多少个?
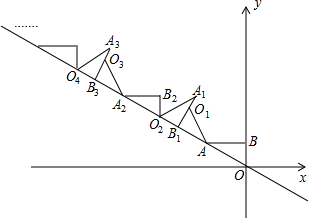 如图,AB⊥y轴,垂足为B,将△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=-$\frac{\sqrt{3}}{3}$x上,再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=-$\frac{\sqrt{3}}{3}$x上,依次进行下去…若点B的坐标是(0,1),则点O12的纵坐标为9+3$\sqrt{3}$.
如图,AB⊥y轴,垂足为B,将△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=-$\frac{\sqrt{3}}{3}$x上,再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=-$\frac{\sqrt{3}}{3}$x上,依次进行下去…若点B的坐标是(0,1),则点O12的纵坐标为9+3$\sqrt{3}$.