题目内容
抛物线y=-x2+(m-1)x+m与y轴交于(0,3),
(1)求m的值;
(2)求抛物线与x轴的交点坐标及顶点坐标;
(3)当x取何值时,抛物线在x轴上方?
(4)当x取何值时,y随x的增大而增大?
(1)求m的值;
(2)求抛物线与x轴的交点坐标及顶点坐标;
(3)当x取何值时,抛物线在x轴上方?
(4)当x取何值时,y随x的增大而增大?
考点:二次函数的性质,二次函数图象上点的坐标特征
专题:
分析:(1)根据图象过点(0,3),则可求出m的值;
(2)利用(1)中所求得出二次函数解析式,进而求出其顶点坐标和与x轴的交点坐标;
(3)画出函数图象进而得出抛物线在x轴上方时,x的取值范围;
(4)利用函数开口方向以及对称轴位置,进而得出y随x的增大而增大时x的取值范围.
(2)利用(1)中所求得出二次函数解析式,进而求出其顶点坐标和与x轴的交点坐标;
(3)画出函数图象进而得出抛物线在x轴上方时,x的取值范围;
(4)利用函数开口方向以及对称轴位置,进而得出y随x的增大而增大时x的取值范围.
解答:解:(1)∵抛物线y=-x2+(m-1)x+m与y轴交于(0,3),
∴3=0+(m-1)×0+m,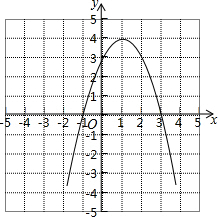
解得:m=3;
(2)∵m=3,
∴抛物线解析式为:y=-x2+2x+3=-(x-1)2+4,
当y=-x2+2x+3=0,
解得:x1=3,x2=-1,
∴抛物线与x轴的交点坐标为:(3,0),(-1,0),
顶点坐标为:(1,4);
(3)如图所示:当-1<x<3时,抛物线在x轴上方;
(4)如图所示:当x<-1时,y随x的增大而增大.
∴3=0+(m-1)×0+m,

解得:m=3;
(2)∵m=3,
∴抛物线解析式为:y=-x2+2x+3=-(x-1)2+4,
当y=-x2+2x+3=0,
解得:x1=3,x2=-1,
∴抛物线与x轴的交点坐标为:(3,0),(-1,0),
顶点坐标为:(1,4);
(3)如图所示:当-1<x<3时,抛物线在x轴上方;
(4)如图所示:当x<-1时,y随x的增大而增大.
点评:此题主要考查了二次函数的性质以及二次函数图象上点的坐标特征,数形结合得出x的取值范围是解题关键.

练习册系列答案
相关题目
如果四条线段a,b,c,d构成
=
,m>0,则下面推理正确的有( )
①
=
;②
=
;③
=
;④
=
.
| a |
| b |
| c |
| d |
①
| a |
| b |
| cm |
| dm |
| a |
| b |
| 7a+cm |
| 7b+dm |
| a |
| b |
| c+m |
| d+m |
| a |
| a+cm |
| b |
| b+dm |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,平面内4条直线L1、L2、L3、L4是一组平行线,相邻2条平行线间的距离都是1个单位长度,正方形ABCD的4个顶点A、B、C、D都在这些平行线上,其中点A、C分别在直线L1和L4上,该正方形的面积是( )平方单位.
如图,平面内4条直线L1、L2、L3、L4是一组平行线,相邻2条平行线间的距离都是1个单位长度,正方形ABCD的4个顶点A、B、C、D都在这些平行线上,其中点A、C分别在直线L1和L4上,该正方形的面积是( )平方单位.| A、4或8 | B、5或8 |
| C、5或9 | D、6或9 |
 在数轴上表示a、b两个实数的点的位置如图,则化简|a-b|-2|a+b|的结果为( )
在数轴上表示a、b两个实数的点的位置如图,则化简|a-b|-2|a+b|的结果为( )| A、-3a-b |
| B、-3a-2b |
| C、3a-b |
| D、-3a+b |
由下列线段a、b、c组成的三角形为直角三角形的是( )
| A、a=15,b=17,c=8 |
| B、a=4,b=5,c=6 |
| C、a=12,b=60,c=61 |
| D、a=12,b=35,c=36 |
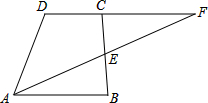 已知:如图,梯形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.
已知:如图,梯形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.