题目内容
15.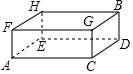 如图,长宽高分别为2,1,1的长方体木块上有一只小虫从顶点A出发沿着长方体的外表面爬到顶点B,则它爬行的最短路程是( )
如图,长宽高分别为2,1,1的长方体木块上有一只小虫从顶点A出发沿着长方体的外表面爬到顶点B,则它爬行的最短路程是( )| A. | $\sqrt{10}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{2}$ | D. | 3 |
分析 蚂蚁有两种爬法,就是把正视和俯视(或正视和侧视)二个面展平成一个长方形,然后求其对角线,比较大小即可求得最短路程.
解答  解:如图所示,
解:如图所示,
路径一:AB=$\sqrt{{2}^{2}+(1+1)^{2}}$=2$\sqrt{2}$;
路径二:AB=$\sqrt{(2+1)^{2}+{1}^{2}}$=$\sqrt{10}$,
∵2$\sqrt{2}$<$\sqrt{10}$,
∴蚂蚁爬行的最短路程为2$\sqrt{2}$.
故选C.
点评 本题考查了立体图形中的最短路线问题;通常应把立体几何中的最短路线问题转化为平面几何中的求两点间距离的问题;注意长方体展开图形应分情况进行探讨.

练习册系列答案
相关题目
5.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{{a}^{2}+{b}^{2}}$ | B. | $\sqrt{\frac{a}{b}}$ | C. | $\sqrt{25a}$ | D. | $\sqrt{4a+4}$ |
6. 如图,把小河里的水引到田地A处就作AB⊥l,垂足为B,沿AB挖水沟,水沟最短,理由是( )
如图,把小河里的水引到田地A处就作AB⊥l,垂足为B,沿AB挖水沟,水沟最短,理由是( )
 如图,把小河里的水引到田地A处就作AB⊥l,垂足为B,沿AB挖水沟,水沟最短,理由是( )
如图,把小河里的水引到田地A处就作AB⊥l,垂足为B,沿AB挖水沟,水沟最短,理由是( )| A. | 垂线段最短 | B. | 两点确定一条直线 | ||
| C. | 点到直线的距离 | D. | 两点之间线段最短 |
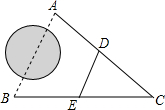 如图,A,B两地无法直接测量距离,现在地面上选一点C,连接CA,CB,分别取CA,CB的中点D,E,若测得DE的长为30m,那么A,B两地间的距离是60m.
如图,A,B两地无法直接测量距离,现在地面上选一点C,连接CA,CB,分别取CA,CB的中点D,E,若测得DE的长为30m,那么A,B两地间的距离是60m.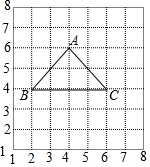 如图,每个小正方形的边长为1个单位,小正方形的顶点叫格点,△ABC的顶点都在格点上,已知点A的方位是(4,6),点B的方位是(2,4).
如图,每个小正方形的边长为1个单位,小正方形的顶点叫格点,△ABC的顶点都在格点上,已知点A的方位是(4,6),点B的方位是(2,4).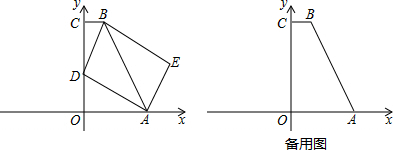
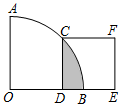 如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2时,阴影部分的面积为π-2.
如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2时,阴影部分的面积为π-2.