题目内容
5．
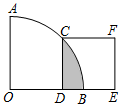如图，在扇形AOB中，∠AOB=90°，正方形CDEF的顶点C是弧AB的中点，点D在OB上，点E在OB的延长线上，当正方形CDEF的边长为2时，阴影部分的面积为π-2．
分析 连结OC，根据勾股定理可求OC的长，根据题意可得出阴影部分的面积=扇形BOC的面积-三角形ODC的面积，依此列式计算即可求解．
解答 
解：连接OC
∵在扇形AOB中∠AOB=90°，正方形CDEF的顶点C是弧AB的中点，
∴∠COD=45°，
∴OC=$\sqrt{2}$CD=2$\sqrt{2}$，
∴阴影部分的面积=扇形BOC的面积-三角形ODC的面积
=$\frac{45×π×（2\sqrt{2}）^{2}}{360}$-$\frac{1}{2}$×22
=π-2．
故答案为π-2．
点评 考查了正方形的性质和扇形面积的计算，解题的关键是得到扇形半径的长度．
练习册系列答案
相关题目
15．
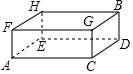如图，长宽高分别为2，1，1的长方体木块上有一只小虫从顶点A出发沿着长方体的外表面爬到顶点B，则它爬行的最短路程是（ ）
如图，长宽高分别为2，1，1的长方体木块上有一只小虫从顶点A出发沿着长方体的外表面爬到顶点B，则它爬行的最短路程是（ ）| A． | $\sqrt{10}$ | B． | $\sqrt{5}$ | C． | 2$\sqrt{2}$ | D． | 3 |
如图，在△ABC中，∠A=90，BD是角平分线，若AD=m，BC=n，则△BDC的面积为$\frac{1}{2}$mn．
10．下列图象中，变量y不是变量x的函数的是（ ）
| A． |  | B． |  | C． |  | D． |  |
14．在5张形状相同的卡片上，分别写有下列5个命题：
①同位角相等；
②三角形中至少有两个锐角；
③三角形三个外角的和是360°；
④三角形中至少有一个角大于60°；
⑤如果两条直线平行，那么同旁内角的平分线互相垂直．
从中任意抽取一张卡片，抽取到卡片写有真命题的概率是（ ）
①同位角相等；
②三角形中至少有两个锐角；
③三角形三个外角的和是360°；
④三角形中至少有一个角大于60°；
⑤如果两条直线平行，那么同旁内角的平分线互相垂直．
从中任意抽取一张卡片，抽取到卡片写有真命题的概率是（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{2}{5}$ | D． | $\frac{1}{5}$ |
如图，已知∠1=∠2，∠B=∠C，可推得AB∥CD．请说明理由．