题目内容
3.用一个圆心角为120°,半径为4的扇形作一个圆锥的侧面,则这个圆锥的底面圆半径为( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
分析 根据扇形的弧长公式求出弧长,根据圆锥的底面周长等于它的侧面展开图的弧长求出半径.
解答 解:设圆锥底面的半径为r,
扇形的弧长为:$\frac{120π×4}{180}$=$\frac{8}{3}$π,
∵圆锥的底面周长等于它的侧面展开图的弧长,
∴根据题意得2πr=$\frac{8}{3}$π,
解得:r=$\frac{4}{3}$.
故选:A.
点评 本题考查的是圆锥的计算,掌握弧长公式、周长公式和圆锥与扇形的对应关系是解题的关键.

练习册系列答案
相关题目
11. 如图,在?ABCD中,BC=10,sinB=$\frac{9}{10}$,AC=BC,则?ABCD的面积是( )
如图,在?ABCD中,BC=10,sinB=$\frac{9}{10}$,AC=BC,则?ABCD的面积是( )
 如图,在?ABCD中,BC=10,sinB=$\frac{9}{10}$,AC=BC,则?ABCD的面积是( )
如图,在?ABCD中,BC=10,sinB=$\frac{9}{10}$,AC=BC,则?ABCD的面积是( )| A. | 2$\sqrt{19}$ | B. | 6$\sqrt{19}$ | C. | 9$\sqrt{19}$ | D. | 18$\sqrt{19}$ |
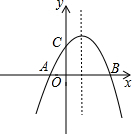 如图,已知二次函数y=-(x+1)(x-m)的图象与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,且图象经过点M(2,3).
如图,已知二次函数y=-(x+1)(x-m)的图象与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,且图象经过点M(2,3). 如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=$\frac{1}{3}$CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为8.
如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=$\frac{1}{3}$CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为8. 如图所示,四边形OABC是矩形,点A、C的坐标分别为(6,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-$\frac{1}{2}$x+m交折线OAB于点E.
如图所示,四边形OABC是矩形,点A、C的坐标分别为(6,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-$\frac{1}{2}$x+m交折线OAB于点E. 如图:把一个矩形如图折叠,使顶点B和D重合,折痕为EF.
如图:把一个矩形如图折叠,使顶点B和D重合,折痕为EF. 如图,△ABC的三个顶点位置分别是A(1,0),B(-2,3),C(-3,0).
如图,△ABC的三个顶点位置分别是A(1,0),B(-2,3),C(-3,0).