题目内容
14. 如图,△ABC的三个顶点位置分别是A(1,0),B(-2,3),C(-3,0).
如图,△ABC的三个顶点位置分别是A(1,0),B(-2,3),C(-3,0).(1)求△ABC的面积;
(2)若点A、C的位置不变,当点P在y轴上什么位置时,使S△ACP=2S△ABC?
(3)若点B、C的位置不变,当点Q在x轴上什么位置时,使S△BCQ=2S△ABC?
分析 (1)根据点A、C的坐标求出AC的长,然后利用三角形的面积列式计算即可得解;
(2)分点P在y轴正半轴和负半轴两种情况讨论求解;
(3)分点Q在C的左边和右边两种情况讨论求解.
解答 解:(1)∵A(1,0),B(-2,3),C(-3,0),
∴AC=1-(-3)=1+3=4,
点B到AC的距离为3,
∴△ABC的面积=$\frac{1}{2}$×4×3=6;
(2)∵S△ACP=2S△ABC,
3×2=6,
∴点P在y轴正半轴时,P(0,6);
点P在y轴负半轴时,P(0,-6);
(3)∵S△BCQ=2S△ABC,
4×2=8,
∴点Q在C的左边时,Q(-3-8,0),即Q(-11,0);
点Q在C的右边时,Q(-3+8,0),即Q(5,0).
点评 本题考查了坐标与图形性质,三角形的面积,难点在于要分情况讨论.

练习册系列答案
相关题目
3.用一个圆心角为120°,半径为4的扇形作一个圆锥的侧面,则这个圆锥的底面圆半径为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
9.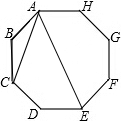 如图,在正八边形ABCDEFGH中,连接AC,AE,则$\frac{AE}{AC}$的值是( )
如图,在正八边形ABCDEFGH中,连接AC,AE,则$\frac{AE}{AC}$的值是( )
 如图,在正八边形ABCDEFGH中,连接AC,AE,则$\frac{AE}{AC}$的值是( )
如图,在正八边形ABCDEFGH中,连接AC,AE,则$\frac{AE}{AC}$的值是( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{3}$ |
4.(-2)×$\frac{1}{2}$=( )
| A. | -2 | B. | 1 | C. | -1 | D. | $\frac{1}{2}$ |
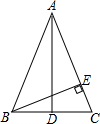 如图,等腰△ABC中,AB=AC,D是底边BC中点,BE⊥AC于E.
如图,等腰△ABC中,AB=AC,D是底边BC中点,BE⊥AC于E.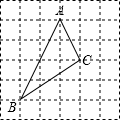 如图,三角形ABC在正方形网格中(图中每个小正方形的边长均为1个单位长度),若点A的坐标为(0,3),点B的坐标为(-2,-1),按要求解下列问题:
如图,三角形ABC在正方形网格中(图中每个小正方形的边长均为1个单位长度),若点A的坐标为(0,3),点B的坐标为(-2,-1),按要求解下列问题: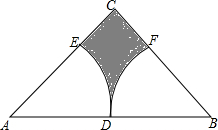 如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD和扇形FBD的圆心分别为点A、点B,且AB=4,则图中阴影部分的面积为4-π(结果保留π).
如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD和扇形FBD的圆心分别为点A、点B,且AB=4,则图中阴影部分的面积为4-π(结果保留π).