题目内容
3.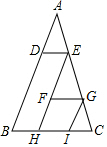 如图,在△ABC中,DE∥FG∥BC,GI∥EF∥AB,若△ADE、△EFG、△GIC的面积分别为8cm2、32cm2、18cm2,则△ABC的面积为162cm2.
如图,在△ABC中,DE∥FG∥BC,GI∥EF∥AB,若△ADE、△EFG、△GIC的面积分别为8cm2、32cm2、18cm2,则△ABC的面积为162cm2.
分析 根据DE∥FG∥BC、GI∥EF∥AB即可得出∠AED=∠EGF=∠GCI、∠A=∠FEG=∠IGC,由此即可得出△ADE∽△EFG∽△GIC∽△ABC,根据△ADE、△EFG、△GIC的面积分别为8cm2、32cm2、18cm2,即可得出AE:EG:GC=2:4:3,即AE:AC=2:9,再根据相似三角形的性质即可得出S△ABC=$(\frac{AC}{AE})^{2}$•S△ADE,代入数据即可得出结论.
解答 解:∵DE∥FG∥BC,
∴∠AED=∠EGF=∠GCI,
∵GI∥EF∥AB,
∴∠A=∠FEG=∠IGC,
∴△ADE∽△EFG∽△GIC∽△ABC,
∵△ADE、△EFG、△GIC的面积分别为8cm2、32cm2、18cm2,
∴AE:EG:GC=2:4:3,
∴AE:AC=2:9,
∴S△ABC=$(\frac{AC}{AE})^{2}$•S△ADE=$(\frac{9}{2})^{2}$×8=162.
故答案为:162.
点评 本题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质定理是解题的关键.

练习册系列答案
相关题目
14. 如图,平行四边形ABCD中,BE平分∠ABC交AD于E点,已知AB=5,AD=6,则DE长为( )
如图,平行四边形ABCD中,BE平分∠ABC交AD于E点,已知AB=5,AD=6,则DE长为( )
 如图,平行四边形ABCD中,BE平分∠ABC交AD于E点,已知AB=5,AD=6,则DE长为( )
如图,平行四边形ABCD中,BE平分∠ABC交AD于E点,已知AB=5,AD=6,则DE长为( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
15.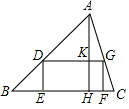 如图,△ABC中,点E、F在BC边上,点D,G分别在AB,AC边上,四边形DEFG是矩形,若矩形DEFG面积与△ADG的面积相等,设△ABC的BC边上高AH与DG相交于点K,则$\frac{DG}{BC}$的值为( )
如图,△ABC中,点E、F在BC边上,点D,G分别在AB,AC边上,四边形DEFG是矩形,若矩形DEFG面积与△ADG的面积相等,设△ABC的BC边上高AH与DG相交于点K,则$\frac{DG}{BC}$的值为( )
 如图,△ABC中,点E、F在BC边上,点D,G分别在AB,AC边上,四边形DEFG是矩形,若矩形DEFG面积与△ADG的面积相等,设△ABC的BC边上高AH与DG相交于点K,则$\frac{DG}{BC}$的值为( )
如图,△ABC中,点E、F在BC边上,点D,G分别在AB,AC边上,四边形DEFG是矩形,若矩形DEFG面积与△ADG的面积相等,设△ABC的BC边上高AH与DG相交于点K,则$\frac{DG}{BC}$的值为( )| A. | 1:1 | B. | 1:2 | C. | 2:3 | D. | $\sqrt{2}$:3 |
13.若圆的半径为5,圆心的坐标是(0,0),点P的坐标是(4,3),则点P与⊙O的位置关系是( )
| A. | 点P在⊙O上 | B. | 点P在⊙O内 | C. | 点P在⊙O外 | D. | 点P不在⊙O上 |
 如图所示,已知:点D在△ABC的边AB上,连结CD,∠1=∠B,AD=4,AC=5,求AB的长.
如图所示,已知:点D在△ABC的边AB上,连结CD,∠1=∠B,AD=4,AC=5,求AB的长.