题目内容
7.已知:x=$\sqrt{5}$$+\sqrt{3}$,y=$\sqrt{5}$$-\sqrt{3}$,求x2-xy+y2和$\frac{x}{y}$$+\frac{y}{x}$的值.分析 先计算x+y、xy的值,再整体代入到x2-xy+y2=(x+y)2-3xy、$\frac{x}{y}$$+\frac{y}{x}$=$\frac{(x+y)^{2}-2xy}{xy}$计算可得.
解答 解:∵x=$\sqrt{5}$$+\sqrt{3}$,y=$\sqrt{5}$$-\sqrt{3}$,
∴x+y=2$\sqrt{5}$,xy=($\sqrt{5}$)2-($\sqrt{3}$)2=2,
则x2-xy+y2=(x+y)2-3xy
=(2$\sqrt{5}$)2-3×2
=14,
$\frac{x}{y}$$+\frac{y}{x}$=$\frac{{x}^{2}+{y}^{2}}{xy}$
=$\frac{(x+y)^{2}-2xy}{xy}$
=$\frac{(2\sqrt{5})^{2}-2×2}{2}$
=8.
点评 本题主要考查了二次根式的化简求值,观察原式的特点,采用通用的、简便的方法是解题的关键.

练习册系列答案
相关题目
19.下列说法正确的是( )
| A. | 若两个角互补,则一个角是锐角,一个角是钝角 | |
| B. | 有一个公共顶点的角是对顶角 | |
| C. | 若两个角互余,则这两个角一定都是锐角 | |
| D. | 两个锐角一定互为余角 |
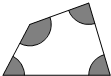 如图,已知四个扇形的半径均为1,那么图中阴影部分面积的和是π.
如图,已知四个扇形的半径均为1,那么图中阴影部分面积的和是π.