题目内容
如图,点B在射线AE上,△CBA沿射线AE翻折后能与⊿DBA重合,则正确的是( )
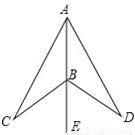
A. CA=DB B. ∠CAE=∠DBE C. AC=AD D. ∠CBA=∠DBE
 C
【解析】∵△CBA沿射线AE翻折后能与△DBA重合,
∴∠D=∠C,∠CAB=∠DAB,∠CBA=∠DBA,AC=AD,
故选C.
C
【解析】∵△CBA沿射线AE翻折后能与△DBA重合,
∴∠D=∠C,∠CAB=∠DAB,∠CBA=∠DBA,AC=AD,
故选C.
练习册系列答案
相关题目
一个袋中装有2个红球,3个蓝球和5个白球,它们除颜色外完全相同,现在从中任意摸出一个球,则P(摸到红球)等于( )
A. 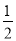 B.
B. 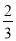 C.
C. 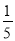 D.
D. 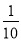
 C
【解析】袋中有2个红球,3个蓝球和5个白球,故共有球10个,所以从中任意摸出一个球,则P(摸到红球)=,故选C.
C
【解析】袋中有2个红球,3个蓝球和5个白球,故共有球10个,所以从中任意摸出一个球,则P(摸到红球)=,故选C. 一个等腰三角形两边的长分别是15cm和7cm则它的周长是__________.
 37cm
【解析】①7cm是腰长时,三角形的三边分别为7cm、7cm、15cm,
∵7+7=14<15,
∴不能组成三角形,
②7cm是底边时,三角形的三边分别为7cm、15cm、15cm,
能组成三角形,
周长=7+15+15=37cm,
综上所述,它的周长是37cm.
故答案为:37cm.
37cm
【解析】①7cm是腰长时,三角形的三边分别为7cm、7cm、15cm,
∵7+7=14<15,
∴不能组成三角形,
②7cm是底边时,三角形的三边分别为7cm、15cm、15cm,
能组成三角形,
周长=7+15+15=37cm,
综上所述,它的周长是37cm.
故答案为:37cm. 已知△ABC≌△A′B′C′,∠C=25°,BC=6 cm,AC=4 cm,你能得出△A′B′C′中哪些角的大小,哪些边的长度?
 ∠C’=25°,B’C’=6 cm,A’C’=4cm
【解析】试题分析:根据全等三角形的性质即可得.
试题解析:∵△ABC≌△A′B′C′,
∴∠C′=∠C=25°,
B′C′=BC=6cm,
A′C′=AC=4cm.
∠C’=25°,B’C’=6 cm,A’C’=4cm
【解析】试题分析:根据全等三角形的性质即可得.
试题解析:∵△ABC≌△A′B′C′,
∴∠C′=∠C=25°,
B′C′=BC=6cm,
A′C′=AC=4cm. 如图,△ABD≌△ACE,AE=3cm,AC=6 cm,则CD=__________cm.
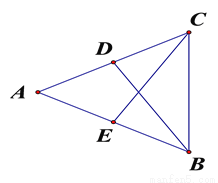
 3
【解析】∵△ABD≌△ACE,
∴AD=AE=3cm,
∴CD=AC-AD=6 -3=3cm,
故答案为:3.
3
【解析】∵△ABD≌△ACE,
∴AD=AE=3cm,
∴CD=AC-AD=6 -3=3cm,
故答案为:3. 如图,△AOD关于直线 进行轴对称变换后得到△BOC,下列不正确的是().
进行轴对称变换后得到△BOC,下列不正确的是().
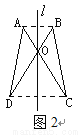
A. ∠DAO=∠CBO,∠ADO=∠BCO B. 直线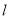 垂直平分AB、CD
垂直平分AB、CD
C. △AO D和△BOC均是等腰三角形 D. AD=BC,OD=OC
 C
【解析】试题分析:根据轴对称图形的性质可得:A、B、D为正确答案;△OAB和△DOC为等腰三角形.
C
【解析】试题分析:根据轴对称图形的性质可得:A、B、D为正确答案;△OAB和△DOC为等腰三角形. 如下图所示,判断各组中的两个图形是否是全等图形.
A. 
B. 
C. 
D. 
 A
【解析】全等图形需要大小相等,形状相同,原图中只有A同时符合这两个条件,B、C、D都只是形状相同,但大小不相等,
故选A.
A
【解析】全等图形需要大小相等,形状相同,原图中只有A同时符合这两个条件,B、C、D都只是形状相同,但大小不相等,
故选A. 如图,在空白网格内将某一个小正方形涂成阴影部分,且所涂的小正方形与原阴影图形的小正方形至少有一边重合.小红按要求涂了一个正方形,所得到的阴影图形恰好是轴对称图形的概率为( )

A. B.
B. C.
C.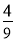 D.
D.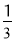
 C.
【解析】
试题分析:如图所示:所涂的小正方形与原阴影图形的小正方形至少有一边重合的一共有9个,
能构成轴对称图形的有所标数据1,2,3,4,共4个,则所得到的阴影图形恰好是轴对称图形的概率为:.
故选:C.
C.
【解析】
试题分析:如图所示:所涂的小正方形与原阴影图形的小正方形至少有一边重合的一共有9个,
能构成轴对称图形的有所标数据1,2,3,4,共4个,则所得到的阴影图形恰好是轴对称图形的概率为:.
故选:C. (2011•江津区)在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
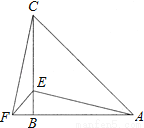
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
 (1)见解析;(2)60°.
【解析】
试题分析:(1)由AB=CB,∠ABC=90°,AE=CF,即可利用HL证得Rt△ABE≌Rt△CBF;
(2)由AB=CB,∠ABC=90°,即可求得∠CAB与∠ACB的度数,即可得∠BAE的度数,又由Rt△ABE≌Rt△CBF,即可求得∠BCF的度数,则由∠ACF=∠BCF+∠ACB即可求得答案.
(1)证明:∵∠ABC=90°,...
(1)见解析;(2)60°.
【解析】
试题分析:(1)由AB=CB,∠ABC=90°,AE=CF,即可利用HL证得Rt△ABE≌Rt△CBF;
(2)由AB=CB,∠ABC=90°,即可求得∠CAB与∠ACB的度数,即可得∠BAE的度数,又由Rt△ABE≌Rt△CBF,即可求得∠BCF的度数,则由∠ACF=∠BCF+∠ACB即可求得答案.
(1)证明:∵∠ABC=90°,... 
