题目内容
16.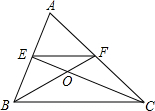 如图,在△ABC中,点E,F分别为AB,AC的中点,连接CE,BF,相交于点O.若△OEF的面积为1,则△ABC的面积为( )
如图,在△ABC中,点E,F分别为AB,AC的中点,连接CE,BF,相交于点O.若△OEF的面积为1,则△ABC的面积为( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
分析 由E、F分别为边AC、AB的中点,可知FE=$\frac{1}{2}$BC,EF∥BC;从而可判定△FEO∽△CBO,根据相似三角形面积的比等于相似比的平方,及已知△OEF的面积为1,即可求得△BCO、△BOE、△COF的面积,即可得到四边形EBCF的面积,即可得到结果.
解答 解:∵E、F分别为边AC、AB的中点,
∴FE=$\frac{1}{2}$BC,EF∥BC;
∴△FEO∽△CBO,
∴$\frac{OE}{OC}$=$\frac{EF}{BC}$=$\frac{OF}{OB}$=$\frac{1}{2}$,
∵相似三角形面积的比等于相似比的平方,
∴△OEF的面积:△BCO的面积=1:4;
∵△OEF的面积为1,
∴△BCO的面积为4,
∴△OFC的面积=△OBE的面积=2△OEF的面积=2,
∴四边形EBCF的面积=9,
∵△AEF的面积:△ABC的面积=$({\frac{EF}{BC})}^{2}$=$\frac{1}{4}$,
∴四边形EBCF的面积:△ABC的面积=3:4,
∴△ABC的面积=12.
故选D.
点评 本题主要考查了三角形中位线定理,相似三角形的判定和性质,三角形的面积,掌握定理是解题的关键.

练习册系列答案
相关题目
7.在一次中学生田径运动会上,参加跳高的15名运动员的成绩如表:
那么这些运动员跳高成绩的中位数是( )
| 成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 1 | 2 | 3 | 4 | 3 | 2 |
| A. | 4 | B. | 1.65 | C. | 1.70 | D. | 3 |
6.一组数据2、5、5、5、8、8、9的众数是( )
| A. | 2 | B. | 5 | C. | 8 | D. | 9 |
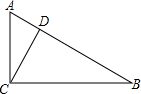 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,AC=6,AD=3.6,则BC=8.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,AC=6,AD=3.6,则BC=8. 如图,AB是⊙O的直径,P在BA的延长线上,过P作⊙O的切线,当D为$\widehat{AE}$中点时,试判断△PBC的形状.
如图,AB是⊙O的直径,P在BA的延长线上,过P作⊙O的切线,当D为$\widehat{AE}$中点时,试判断△PBC的形状.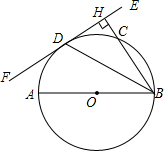 已知:如图,AB为⊙O的直径,C、D是⊙O上两点,BD平分∠ABC,BC的延长线与过点D的直线交于点H,且BH⊥DH.
已知:如图,AB为⊙O的直径,C、D是⊙O上两点,BD平分∠ABC,BC的延长线与过点D的直线交于点H,且BH⊥DH.