题目内容
11．
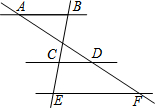如图，已知AB∥CD∥EF，AD：AF=3：5，BE=12，那么CE的长等于（ ）| A． | $\frac{36}{5}$ | B． | $\frac{24}{5}$ | C． | $\frac{15}{2}$ | D． | $\frac{9}{2}$ |
分析 根据平行线分线段成比例得到$\frac{BC}{12}$=$\frac{3}{5}$，然后利用比例性质计算出BC=$\frac{36}{5}$，然后利用计算BE-BC即可．
解答 解：∵AB∥CD∥EF，
∴$\frac{BC}{BE}$=$\frac{AD}{AF}$，即$\frac{BC}{12}$=$\frac{3}{5}$，
∴BC=$\frac{36}{5}$，
∴CE=BE-BC=12-$\frac{36}{5}$=$\frac{24}{5}$．
故选B．
点评 本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．
练习册系列答案
相关题目
如图，AB是⊙O的直径，P在BA的延长线上，过P作⊙O的切线，当D为$\widehat{AE}$中点时，试判断△PBC的形状．
2．
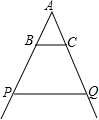如图是小刘做的一个风筝支架示意图，已知BC∥PQ，AB：AP=2：5，BC=20cm，则PQ的长是（ ）
如图是小刘做的一个风筝支架示意图，已知BC∥PQ，AB：AP=2：5，BC=20cm，则PQ的长是（ ）| A． | 45cm | B． | 50cm | C． | 60cm | D． | 80cm |
6．一组数据2、5、5、5、8、8、9的众数是（ ）
| A． | 2 | B． | 5 | C． | 8 | D． | 9 |
3．下列计算正确的是（ ）
| A． | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B． | $\sqrt{2}+\sqrt{3}=\sqrt{6}$ | C． | $5\sqrt{3}-3\sqrt{3}=2$ | D． | $\sqrt{12}÷\sqrt{3}=2$ |