题目内容
 已知△ABC是边长为6的等边三角形,动点P、Q同时分别从A、C两点出发,分别沿AB、CB两点出发,并沿AB、CB匀速运动,其中点P的运动速度是每秒1cm,点Q的运动速度是每秒2cm,当点Q到达B时,P、Q两点都停止运动,作QR∥BA交AC于点R,连接PR.设运动时间为t(s),当t为何值时,四边形PRQB是平行四边形?
已知△ABC是边长为6的等边三角形,动点P、Q同时分别从A、C两点出发,分别沿AB、CB两点出发,并沿AB、CB匀速运动,其中点P的运动速度是每秒1cm,点Q的运动速度是每秒2cm,当点Q到达B时,P、Q两点都停止运动,作QR∥BA交AC于点R,连接PR.设运动时间为t(s),当t为何值时,四边形PRQB是平行四边形?考点:等边三角形的性质,平行四边形的判定与性质
专题:动点型
分析:根据平行四边形的性质和判定方法知:当QR∥AB时四边形PBQR是平行四边形,据此列出方程求解即可.
解答:解:∵点P的运动速度是每秒1cm,点Q的运动速度是每秒2cm,
∴PB=6-t,CQ=2t,
∵△ABC是等边三角形,PB‖RQ,
∴△RQC是等边三角形,
∴QR=CQ=2t,
∵只要使PB=RQ时,四边形PRQB是平行四边形,
即6-t=2t,
得t=2,
∴当t为2时,四边形PRQB是平行四边形.
∴PB=6-t,CQ=2t,
∵△ABC是等边三角形,PB‖RQ,
∴△RQC是等边三角形,
∴QR=CQ=2t,
∵只要使PB=RQ时,四边形PRQB是平行四边形,
即6-t=2t,
得t=2,
∴当t为2时,四边形PRQB是平行四边形.
点评:本题考查了平行四边形的判定与性质及等边三角形的性质的知识,解题的关键是了解平行四边形的判定定理,难度不大.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
下列命题是真命题的是( )
A、-
| ||||
B、若分式方程
| ||||
| C、等腰梯形的同一底上两角相等 | ||||
| D、同位角相等 |
若关于x的方程
-
=1有增根,则m的值是( )
| m |
| x-1 |
| x |
| x-1 |
| A、3 | B、2 | C、1 | D、0 |
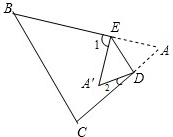 如图,把△ABC纸片沿DE折叠,点A落在四边形BCDE内部.
如图,把△ABC纸片沿DE折叠,点A落在四边形BCDE内部. 如图所示,已知四边形ABCD内接于⊙O,A是弧BAC的中点,AE⊥AC于A,与⊙O及CB的延长线分别交于点F、E,且BF=AD,EM切⊙O于M.
如图所示,已知四边形ABCD内接于⊙O,A是弧BAC的中点,AE⊥AC于A,与⊙O及CB的延长线分别交于点F、E,且BF=AD,EM切⊙O于M.