题目内容
2. 如图,在四边形ABCD中,AB∥CD,∠ABC、∠BCD的平分线交AD于点E.求证:AB+CD=BC.
如图,在四边形ABCD中,AB∥CD,∠ABC、∠BCD的平分线交AD于点E.求证:AB+CD=BC.
分析 先利用角平分线的特点构造出△ABE≌△FBE,得出∠BAE=∠BFE,借助平行线的性质判断出∠CFE=∠CDE,得出△FCE≌△DCE即可.
解答 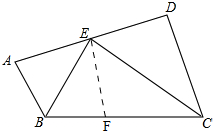 证明:在BC上截取BF=AB,
证明:在BC上截取BF=AB,
∵∠ABC、∠BCD的平分线交AD于点E,
∴∠ABE=∠FBE,∠BCE=∠DCE,
在△ABE和△FBE中$\left\{\begin{array}{l}{AB=BF}\\{∠ABE=∠FBE}\\{BE=BE}\end{array}\right.$,
∴△ABE≌△FBE,
∴∠BAE=∠BFE,
∵AB∥CD,
∴∠BAE+∠CDE=180°,
∴∠BFE+∠CDE=180°,
∵∠BFE+∠CFE=180°,
∴∠CFE=∠CDE,
在△FCE和△DCE中,$\left\{\begin{array}{l}{∠CFE=∠CDE}\\{∠FCE=∠DCE}\\{CE=CE}\end{array}\right.$,
∴△FCE≌△DCE,
∴CF=CD,
∴BC=BF+CF=AB+CD.
点评 此题是全等三角形的性质和判定,主要考查了角平分线的定义,平行线的性质,同角或等角的补角相等,邻补角的定义,解本题的关键是判断出∠CFE=∠CDE.

练习册系列答案
相关题目
6.式子$\sqrt{x-2}$是二次根式,那么( )
| A. | x≠2 | B. | x>2 | C. | x<2 | D. | x≥2 |

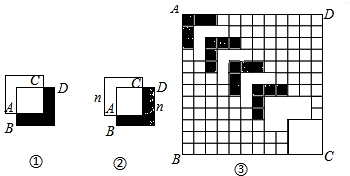
 已知,如图:?ABCD中,对角线相交于O点,AB⊥AC,AB=AC,沿对角线AC将△ABC翻折至△AEC,EC与AD相交于F.
已知,如图:?ABCD中,对角线相交于O点,AB⊥AC,AB=AC,沿对角线AC将△ABC翻折至△AEC,EC与AD相交于F. 已知∠MAN.
已知∠MAN.