题目内容
5.已知,抛物线y=ax2(a≠0)经过点A(4,4),(1)求抛物线的解析式;
(2)如图1,抛物线上存在点B,使得△AOB是以AO为直角边的直角三角形,请直接写出所有符合条件的点B的坐标:B(-4,4)或(-8,16).
(3)如图2,直线l经过点C(0,-1),且平行与x轴,若点D为抛物线上任意一点(原点O除外),直线DO交l于点E,过点E作EF⊥l,交抛物线于点F,求证:直线DF一定经过点G(0,1).

分析 (1)利用待定系数法求出抛物线解析式,
(2)分两种情况,先确定出直线OB或AB,和抛物线解析式联立确定出点B的解析式;
(3)先设出点D坐标,确定出点F坐标,进而得出直线DF解析式,将点G坐标代入直线DF看是否满足解析式.
解答 解:(1)∵抛物线y=ax2(a≠0)经过点A(4,4),
∴16a=4,
∴a=$\frac{1}{4}$,
∴抛物线的解析式为y=$\frac{1}{4}$x2,
(2)存在点B,使得△AOB是以AO为直角边的直角三角形,
理由:如图1,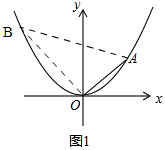
∵使得△AOB是以AO为直角边的直角三角形
∴直角顶点是点O,或点A,
①当直角顶点是点O时,过点O作OB⊥OA,交抛物线于点B,
∵点A(4,4),
∴直线OA解析式为y=x,
∴直线OB解析式为y=-x,
∵$\left\{\begin{array}{l}{y=\frac{1}{4}{x}^{2}}\\{y=-x}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$(舍)或$\left\{\begin{array}{l}{x=-4}\\{y=4}\end{array}\right.$,
∴B(-4,4),
②当直角顶点为点A,过点A作AB⊥OA,
由①有,直线OA的解析式为y=x,
∵A(4,4),
∴直线AB解析式为y=-x+8,
∵$\left\{\begin{array}{l}{y=\frac{1}{4}{x}^{2}}\\{y=-x+8}\end{array}\right.$,
$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$(舍)或$\left\{\begin{array}{l}{x=-8}\\{y=16}\end{array}\right.$,
∴B(-8,16),
∴满足条件的点B(-4,4)或(-8,16);
故答案为B(-4,4)或(-8,16);
(3)证明:设点D(m,$\frac{1}{4}$m2),
∴直线DO解析式为y=$\frac{m}{4}$x,
∵l∥x轴,C(0,-1),
令y=-1,则x=-$\frac{4}{m}$,
∴直线DO与l交于E(-$\frac{4}{m}$,-1),
∵EF⊥l,l∥x轴,
∴F横坐标为-$\frac{4}{m}$,
∵点F在抛物线上,
∴F(-$\frac{4}{m}$,$\frac{4}{{m}^{2}}$)
设直线DF解析式为y=kx+b,
∴$\left\{\begin{array}{l}{-\frac{4}{m}k+b=\frac{4}{{m}^{2}}}\\{mk+b=\frac{{m}^{2}}{4}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=\frac{{m}^{2}-4}{4m}}\\{b=1}\end{array}\right.$,
∴直线DF解析式为y=$\frac{{m}^{2}-4}{4m}$x+1,
∴点G(0,1)满足直线DF解析式,
∴直线DF一定经过点G.
点评 此题是二次函数综合题,主要考查了待定系数法,函数图象的交点坐标,直角三角形的性质,判断点是否在直线上,解本题的关键是确定出点B的坐标,确定出直线DF的解析式是解本题的难点.

 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案| A. | ∠α>∠β | B. | ∠α<∠β | C. | 互余 | D. | 互补 |
| A. | 对某班50名同学身高情况的调查 | |
| B. | 对阜阳市泉河水质情况的调查 | |
| C. | 对端午节市场上粽子质量情况的调查 | |
| D. | 对某类烟花爆竹燃放安全情况的调查 |
| A. | 3 | B. | -3 | C. | ±3 | D. | $\frac{1}{3}$ |
| A. | (2,-1) | B. | (1,2) | C. | (-2,-1) | D. | (-1,2) |
 为了解某中学300名男生的身高情况,随机抽取若干名男生进行身高测量,将所得数据整理后,画出如图所示的频数分布直方图(每组数据包含最大值,不包含最小值),估计该校这300名男生的身高满足:164.5cm<身高≤174.5cm的人数约有( )
为了解某中学300名男生的身高情况,随机抽取若干名男生进行身高测量,将所得数据整理后,画出如图所示的频数分布直方图(每组数据包含最大值,不包含最小值),估计该校这300名男生的身高满足:164.5cm<身高≤174.5cm的人数约有( )| A. | 12 | B. | 16 | C. | 28 | D. | 168 |
| A. | (2,1) | B. | (1,1) | C. | (-2,1) | D. | (4,-2) |

 如图,在四边形ABCD中,AB∥CD,∠ABC、∠BCD的平分线交AD于点E.求证:AB+CD=BC.
如图,在四边形ABCD中,AB∥CD,∠ABC、∠BCD的平分线交AD于点E.求证:AB+CD=BC.