Question

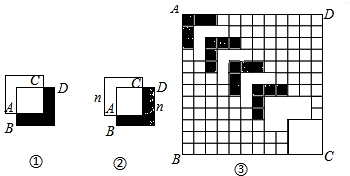
7．【问题】（1）如图①，边长为3cm的两个相同的正方形纸片重叠放置，重叠部分为正方形，两个正方形两条边的交点分别为点A，C，当CD=1cm时，阴影部分的面积为5cm²．
（2题（1）中，设两个正方形的边长都是n（cm）（n＞1），当CD=1cm时（图②），阴影部分的面积为n²-（n-1）²cm²（用n来表示）．
【应用】如图③，12×12cm的方格纸中，每个小正方形的边长都是1cm，现用边长为n（cm）（n是正整数）的大小相同的黑白两种正方形纸片沿对角线方向重叠放置盖住方格纸，重叠部分为正方形且边长都是（n-1）cm（2≤n≤12），第一张纸片放置方格纸的左上角，盖住的面积为n²（cm²），最后一张纸片放置方格纸的右下角，需要的正方形纸片的总数为y（张）．
（1）当n=2时，y=11；
（2）当n=3时，y=10；
（3）求y与n之间的函数关系式．
【探究】方格纸中，被盖住的面积为S₁，未盖住的面积为S₂，是否存在使S₁=S₂的n的值？若存在，求n的值；若不存在，请说明理由．

Answer 1

分析 【问题】（1）（2）：图①②中，用原有一块正方形的面积减去一个重合的小正方形的面积即可求解，
【应用】：图③，（1）当n=2时，计算正方形的张数，可先云去掉最下面的一张，再来计算需要小正方形的纸片数，依次每向上一行需要一张纸片共10行，所以共用纸片10+1=11张；（2）当n=3时，计算方法相同，共用纸片数为9+1=10张；（3）当n=n时，共用的纸片数为12-n+1=13-n，即y=13-n；
【探究】归纳与总结，得到其中的规律．

解答 （1）根据题意，当n=2时，可得应盖住正方形有ABCD对角线上的12个格，
∴y=12-2+1=11，
（2）当n=3时，可得应盖住正方形有ABCD对角线上的13个格，
∴y=12-3+1=10，
故答案为：（1）11，（2）10
（3）当n=n时，可得应盖住正方形有ABCD对角线上的13个格，
∴y=12-n+1=13-n，
探究：第一个面积为n²，第二个面积为一个包边，共有12-n个，每个由2n-1个小正方形构成，包边的总面积为：（12-n）×（2n-1），
∴①S₁=10×3+4=34，S₂=144-34=110，
∴S₁：S₂=34：110=17：55．
②根据题意，得
${S}_{1}=（12-n）×（2n-1）+{n}^{2}$；
${S}_{2}=144-（12-n）×（2n-1）-{n}^{2}$，
若S₁=S₂时，
（12-n）×（2n-1）+n²=144-（12-n）×（2n-1）-n²，
解，得n=4或21．
∵2≤n≤11，
∴∴n=21舍去，
故n=4．

点评 本题是归纳与总结类题目，对于几何类题目根据图形的特征是解答问题的关键．