题目内容
10.如图,在平面直角坐标系中,点A(4,a)(A在第一象限)、点B(5,0).连OA,OB,△ABO的面积是7.5.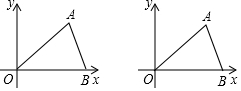
(1)求点A的坐标;
(2)动点P从O点出发,沿射线OA以每秒2个单位长度的速度匀速运动,运动时间t(t>0)秒,连接PB,用含t的式子表示△PAB的面积S,并写出t的取值范围;
(3)在(2)的条件下,点Q在线段AB上,且QB=2AQ,连接PQ,当△APQ的面积为1,求t值并直接写出Q点坐标.
分析 (1)先确定出OB,再利用△AOB的面积求出a即可得出点A坐标;
(2)先确定出AD=3,OD=4,再构造出△ODA∽△OEP得出比例式即可表示出PE,用三角形面积的差即可得出结论;
(3)先求出△PBQ的面积,即可得出△PAB的面积,借助(2)结论即可求出时间t.
解答 解:(1)如图1, 过点A作AD⊥OB于D,
过点A作AD⊥OB于D,
∵B(5,0),
∴OB=5,
∵△ABO的面积是7.5.
∴$\frac{1}{2}$OB•AD=7.5,
∴5AD=15,
∴AD=3,
∴a=3,
∴A(4,3);
(2)如图2,
∵动点P从O点出发,沿射线OA以每秒2个单位长度的速度匀速运动,
∴OP=2t,
由(1)知,AD=3,A(4,3),
∴OA=5,OD=4,
过点A作AD⊥OB于D,过点P作PE⊥OB,
∴AD∥PE,
∴△ODA∽△OEP,
∴$\frac{PE}{AD}=\frac{OP}{OA}$,
∴$\frac{PE}{3}=\frac{2t}{5}$,
∴PE=$\frac{6}{5}$t,
∴S△PAB=S△OAB-S△POB=7.5-$\frac{1}{2}$OB•PE=7.5-$\frac{1}{2}$×5×$\frac{6}{5}$t=7.5-3t(0<t≤2.5);
(3)如图3, ∵QB=2AQ,
∵QB=2AQ,
∴S△PBQ=2S△PAQ=2,
∴S△PAB=3,
由(2)知,S△PAB=7.5-3t=3,
∴t=1.5.
点评 此题是三角形综合题,主要考查了三角形的面积公式,相似三角形的性质和判定,同高的两三角形的面积比是底的比;解(1)的关键是用三角形OAB的面积建立方程求解,解(2)的关键是用相似三角形得出的比例式建立方程表示出PE,解(3)的关键是求出三角形PAB的面积.

练习册系列答案
相关题目
20.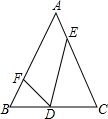 如图,D、E、F分别是等腰三角形ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=$\frac{3}{2}$,∠FDE=∠B,那么AF的长为( )
如图,D、E、F分别是等腰三角形ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=$\frac{3}{2}$,∠FDE=∠B,那么AF的长为( )
 如图,D、E、F分别是等腰三角形ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=$\frac{3}{2}$,∠FDE=∠B,那么AF的长为( )
如图,D、E、F分别是等腰三角形ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=$\frac{3}{2}$,∠FDE=∠B,那么AF的长为( )| A. | 5.5 | B. | 4 | C. | 4.5 | D. | 3.5 |
1.在Rt△ABC中,∠C=90°,当∠A的度数不断增大时,cosA的值的变化情况是( )
| A. | 不断变大 | B. | 不断减小 | C. | 不变 | D. | 不能确定 |
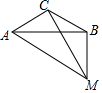 如图,在△ABC中,∠ACB=120°,点M为△ABC外一点,且∠AMB=60°,若CM平分∠AMB.求证:AM+BM=$\sqrt{3}$CM.
如图,在△ABC中,∠ACB=120°,点M为△ABC外一点,且∠AMB=60°,若CM平分∠AMB.求证:AM+BM=$\sqrt{3}$CM.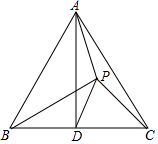 如图,△ABC是等边三角形,点D为BC的中点,点P在△ABC的内部,连接PA、PB、PC、PD,∠BPC=105°,PC=2,PB=2$\sqrt{2}$,则△APD的面积为$\frac{1}{2}\sqrt{3}$.
如图,△ABC是等边三角形,点D为BC的中点,点P在△ABC的内部,连接PA、PB、PC、PD,∠BPC=105°,PC=2,PB=2$\sqrt{2}$,则△APD的面积为$\frac{1}{2}\sqrt{3}$.