题目内容
19.方程x2+ax+b=0的两根为x1,x2,若存在实数a,b使得x13+x23=x12+x22=x1+x2则我们就称这样的两个根(x1,x2)为组“黄金根”,则这样的“黄金根”共有(0,1)、(1,1)或(0,0).2(参考公式:a3+b3=(a+b)[(a+b)2-3ab])分析 根据根与系数的关系即可得出x1+x2=-a、x1•x2=b,将x13+x23=x12+x22=x1+x2变形为(x1+x2)[(x1+x2)2-3x1•x2]=(x1+x2)2-2x1•x2=x1+x2,代入x1+x2=-a、x1•x2=b即可得出关于a、b的方程,解之即可得出a、b的值,将其代入原方程解之即可得出x1、x2的值,此题得解.
解答 解:∵方程x2+ax+b=0的两根为x1,x2,
∴x1+x2=-a,x1•x2=b.
∵x13+x23=(x1+x2)[(x1+x2)2-3x1•x2]=x12+x22=(x1+x2)2-2x1•x2=x1+x2,
∴-a[(-a)2-3b]=(-a)2-2b=-a,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=0}\end{array}\right.$或$\left\{\begin{array}{l}{a=-2}\\{b=1}\end{array}\right.$或$\left\{\begin{array}{l}{a=0}\\{b=0}\end{array}\right.$.
当a=-1、b=0时,原方程为x2-x=0,
解得:x1=0,x2=1;
当a=-2、b=1时,原方程为x2-2x+1=0,
解得:x1=x2=1;
当a=0、b=0时,原方程为x2=0,
解得:x1=x2=0.
故答案为:(0,1)、(1,1)或(0,0).
点评 本题考查了根与系数的关系,根据根与系数的关系结合x13+x23=x12+x22=x1+x2得出-a[(-a)2-3b]=(-a)2-2b=-a是解题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
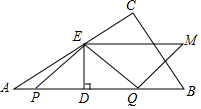 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=3cm,动点P、Q分别从点A、B同时出发,点P以1cm/s的速度沿A→B向终点B运动.点Q以2cm/s的速度沿B→向终点A运动.过QP的中点D作DE⊥AB交AC于点E.将△PQE绕着EQ的中点旋转180°得到△MEQP.设四边形QMEP的面积为S(cm2),点P运动的时间为t(s).
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=3cm,动点P、Q分别从点A、B同时出发,点P以1cm/s的速度沿A→B向终点B运动.点Q以2cm/s的速度沿B→向终点A运动.过QP的中点D作DE⊥AB交AC于点E.将△PQE绕着EQ的中点旋转180°得到△MEQP.设四边形QMEP的面积为S(cm2),点P运动的时间为t(s).
 如图,在?ABCD中,对角线BD、AC交于点O,∠ABD=2∠DBC,AE⊥BD于E.探究线段AB与OE的数量关系.
如图,在?ABCD中,对角线BD、AC交于点O,∠ABD=2∠DBC,AE⊥BD于E.探究线段AB与OE的数量关系. 如图,∠B与∠BCD互为余角,∠B=∠ACD,DE⊥BC,垂足为E,AC与DE平行吗?
如图,∠B与∠BCD互为余角,∠B=∠ACD,DE⊥BC,垂足为E,AC与DE平行吗? 如图,已知HM平分∠EHD,GB∥HD,∠3=35°.
如图,已知HM平分∠EHD,GB∥HD,∠3=35°.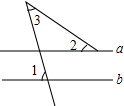 如图,已知∠1=75°,∠2=35°,∠3=40°,则直线a与b的位置关系是平行.
如图,已知∠1=75°,∠2=35°,∠3=40°,则直线a与b的位置关系是平行.